八年级数学下学期复习（二）
班级 姓名 学号 得分
一、选择题（每小题3分，共24分）
1．下列函数中，y是x的反比例函数的是（ ）
（A）y=-
（B）y=-
（Ｃ）y=
（Ｄ）y=1-
2．已知y与x成正比例，z与y成反比例，那么z与x之间的关系是（ ）
（Ａ）成正比例 （B）成反比例 （Ｃ）有可能成正比例，也有可能成反比例 （Ｄ）无法确定
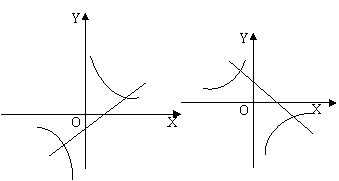
3.如图，函数y=k(x+1)与y=在同一坐标系中，图像只能是下图中的（ ）
 | |||
 | |||
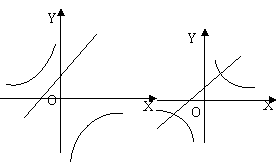（Ａ） （Ｂ） （Ｃ） （Ｄ）
4.已知反比例函数y=
(k﹤0)的图象上有两点A(
,
),B(
,
)，且﹤，则-的值是（ ）
（Ａ）正数 （Ｂ）负数 （Ｃ）非正数 （Ｄ）不能确定
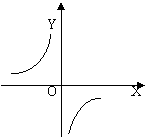
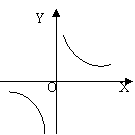
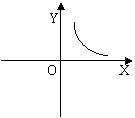
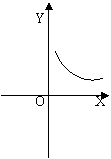5.三角形的面积为4ｃ㎡，底边上的高y(㎝)与底边x(㎝)之间的函数关系图象大致应为( )
 | |||
 | |||
.
(A) (B) (C) (D)
6.已知反比例函数y=的图象经过点（1，2），则函数y=-kx可为( )
（Ａ）y=-2x （Ｂ）y=-
x （Ｃ）y=x
（Ｄ）y=2x
7.对于反比例函数y=
,下列说法不正确的是( )
（Ａ）点（-2,-1）在它的图象上 （Ｂ）它的图象在弟一、三象限
（Ｃ）当x﹥0时，y随x的增大而增大 （D）当x﹤0时，y随x的增大而减少
8.已知（-2，），（-1，）,(1,
)在反比例函数y=-的图象上，则下列结论正确的是（ ）
(A)﹤﹤(B) ﹤﹤(C) ﹥﹥(D) ﹤﹤
二、填空题（每小题4分,共24分）
9.某奶粉生产厂要制造一种容积为2升（1升=1立方分米）的圆柱形桶，桶的底面积s与桶高h有怎样的函数关系式
10．一水桶的下底面积是盖面积的2倍，如果将其底朝下放在桌上，它对桌面的压强是600Pa,翻过来放，对桌面的压强是
11.设有反比例函数y=
,(,)、(,)为其图象上两点，若 ﹤0﹤，﹥，则k的取值范围
12.直线y=kx+b过一、三、四象限，则函数y=
的图象在
象限，并且在每一象限内y随x 的增大而
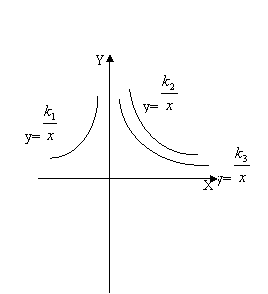13.如图所示是三个反比例函数y=
,y=
,
y=
的图象，由此观察
、
、
的大小关系
是 （用“﹤”连接）
14．若反比例函数的图象经过点（2，-2），（m,1）,
m=
三、解答下列问题
15.已知变量y与（x+1）成反比例，且当x=2时，y=-1,求y和x之间的函数关系。（满分10分）
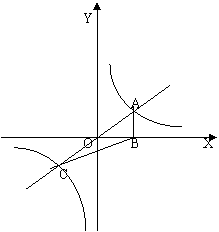
16.如图，正比例函数y=kx(k﹥0)与反比例函数y=
的图象相交于A、C两点，过A作x轴的垂线交x于
B点，连BC,求△ABC的面积。（满分12分）
17.某空调厂的装备车间计划组装9000台空调：
（1）从组装空调开始，每天组装的台数m(单位：台/天)与生产的时间t(单位：天)之间有怎样的函数关系？
（2）原计划用2个月时间（每月以30天计算）完成，由于气温提前升高，厂家决定这批空调提前十天上市，那么装配车间每天至少要组装多少空调？（满分14分）
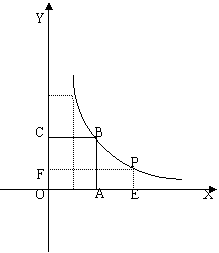
18.如图，正方形OABC的面积为9，点O为坐标原点，点B在函数y=(k﹥0,x﹥0)的图象上，点P（m,n）是函数 y=(k﹥0,x﹥0)的图象上任意一点，过点P分别作x轴、y轴的垂线，垂足分别E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示：考虑点P在点B的左侧或右侧两种情况)
（1）求B点坐标和k的值。
（2）当S=
时，求点P的坐标。
（3）写出S关于m的函数关系式。（满分16分）
测试题参考答案
1～8 A B D D B A C B
9～14
S=
12000Pa k﹤-1 二、四增大
﹤﹤ -4
15. y=-
16. 1
17. (1)m=
(2) 180
18. (1) (3,3) ,K=9 (2) (
,6), (6, )
(3)s=9-
或S=9-3m