八年级数学下学期复习（四）
班级 姓名 学号 得分
一、选择题（每小题3分，共24分）
1.下列命题中正确的是（ ）
A.对角线互相平分的四边形是菱形 B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形 D.对角线互相垂直平分的四边形是菱形
2.某花木场有一块等腰梯形ABCD的空地，其各边的中点分别是E、F、G、H测量得对角线AC=10米，现想用篱笆围成四边形EFGH场地，则需篱笆总长度是（ ）
A. 40米 B. 30米 C.20米 D.10米
3.在梯形ABCD中，AD∥BC,对角线AC⊥BD,且AC=10,BD=6,则该梯形的面积是（ ）
A. 30
B. 15
C.
D.60
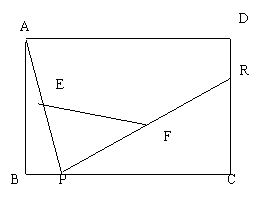
4.如图，已知矩形ABCD,R、P分别是DC、BC上
的点，E、F分别是AP、RP的中点，当P在BC
上从B向C移动而R不动时，那么下列结论成立
的是（ ）
A. 线段Ef的长逐渐增大.B.线段Ef的长逐渐减少
C.线段EF的长不改变. D.线段EF的长不能确定.
5.在平行四边形、矩形、正方形、等腰梯形、直角
梯形中，不是轴对称图形的有（ ）
A. 1个 B.2个 C.3个
D.4个
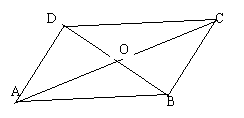
6.如图， ABCD中的两条对角线相交于O点，通过旋转、
平移后，图中能重合的三角形共有（ ）
A.2对 B.3对 C.4对 D.5对
7.菱形的周长为高的8倍，则它的一组邻角是（ ）
A.30°和150° B.45°和135° C.60°和120° D.80°和100°
8.在矩形ABCD中，AB=3,BC=4,则点A到对角线BD的距离为（ ）
A.
B.2
C.
D.
二、填空题（每小题3分，共18分）
9.在平行四边形ABCD中，DB=DC,∠C=70°,AE⊥BD于E,则∠DAE= 度
10.如图，BD是平行四边形ABCD的对角线，点E、F在BD上，要使四边形AECF
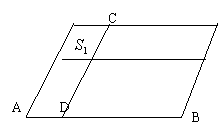
是平行四边形，还需要增加的一个条件是 . （填一个即可）
（9题图） （10题图）
11.如图，一个平行四边形被分成面积为
、、、四个小平行四边形，当CD沿AB自左向右在平行四边形内平行滑动时，则
与的大小关系为 .
12．若梯形的面积为12c
,高为3cm,则此中位线长为
.
13.对角线 的四边形是菱形.
14.在梯形ABCD中，DC∥AB,DC+CB=AB,且∠A=51°,则∠B的度数是 .
三.解答题
|
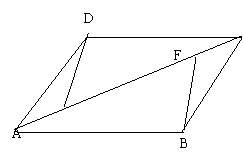
15.(10分)已知：如图，在平行四边形ABCD中，
E、F是对角线AC上的两点，且AE=CF.
求证：DE=BF E
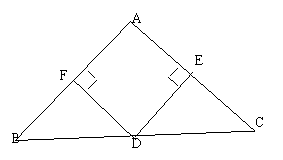16．(18分)已知：如图，D是△ABC的BC边上的中点，DE⊥AC,DF⊥AB,
垂足分别是E、F,且BF=CE.
求证：（1）△ABC是等腰三角形；
（2）当∠A=90°时，试判断四边形AFDE是
怎样的四边形，证明你的判断结论.
17.(10分)如图，已知直线m∥n,A、B为直线n上的两点，C、P为直线m上的两
 |
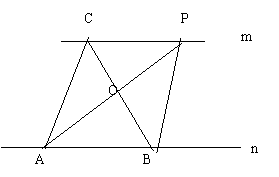点.(1)请写出图中面积相等的各对三角形：
.
(2)如果A、B、C为三个定点，点P在m上移动
那么无论P点移动到任何位置时总有
与△ABC的面积相等；
理由是： .
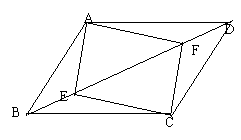
18.（10分）如图，在菱形ABCD中，E为AD中点，
EF⊥AC交CB的延长线于F.
求证：AB与EF互相平分
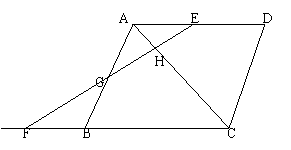
19.(14分)如图，以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF,
 |
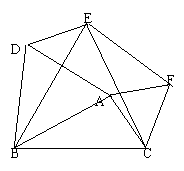请回答下列问题：
（1） 求证：四边形ADEF是平行四边形；
（2） 当△ABC满足什么条件时，四边形ADEF是矩形.
测试题参考答案
1～8 D C A C
B C A A
9～14 20 BE=DF(不唯一) =
4 互相垂直平分 78°
15. 略
16. (1) 略
(2)AFDE是正方形
17．(1)△ABC和△ABP, △AOC和△BOP,△CPA和△CPB;
(2) △ABP,
(3)同底等高
18.略
19. (1)略
(2)150°