| 座 号 |
|
|
八年级数学第二学期阶段考试试卷
| 题号 | 一 | 二 | 三 | 合计 | ||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得分 | ||||||||||||
（考查内容：第十七章 反比例函数）
说明：1、全卷共8页。考试时间90分钟，满分150分．
2、答卷前，考生必须将自己的座号、姓名、班级、学校按要求填写在密封线左边的空格内。
3、答题可用黑色钢笔、圆珠笔按各题要求答在试卷上，但不能用铅笔或红笔
| 姓 名 |
|
|
第Ⅰ部分 选择题（共30分）
| 得分 | 评卷人 |
|
|
|
一、选择题（本题共10小题，每小题3分，共30分．每小题给出的4 个选项中只有一个是符合题目要求的。）
1、下列函数中，反比例函数是（ ）
（A） 
（B）
（C） 
（D） 
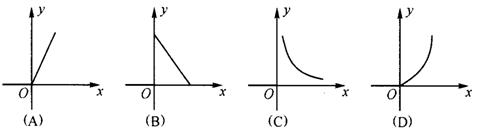
2、某村的粮食总产量为a（a为常数）吨，设该村的人均粮食产量为y
吨，人口数为x，则y与x之间的函数关系式的大致图像应为（ ）
| 班 级 |
|
|
3、若
与－3
成反比例，与
成反比例，则是
的（ ）
（A）正比例函数 （B）反比例函数 （C）一次函数 （D）不能确定
| 学 校 |
|
|
4、若反比例函数
的图像在第二、四象限，则
的值是（ ）
（A）－1或1
（B）小于
的任意实数 （C） －1 （Ｄ） 不能确定
5、已知反比例函数的图像经过点（
，
），则它的图像一定也经过（ ）
（A）(－,－) （B）(,－)
（C）(－，)
（D）（0，0）
6、若M(
,
)、N(
,
)、P(
,
)三点都在函数
（k>0）的图象上，则、、的大小关系是（ ）
（A）
（B）
（C） 
（D）
7、如图，A为反比例函数图象上一点，AB垂直轴于B点，若
＝5，则
的值为（
）
（A）
10 （B） 
（C） 
（D）
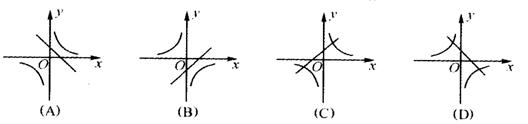
8、在同一直角坐标系中，函数y=kx-k与
的图像大致是（ ）
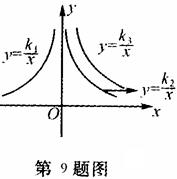9、如图是三个反比例函数
，在x轴上方的图像，由此观察得到kl、k2、k3的大小关系为（ ）
（A） k1>k2>k3 （B） k3>k1>k2
（C） k2>k3>k1 （D） k3>k2>k1
10、在同一直角坐标平面内，如果直线
与双曲线
没有交点，那么
和
的关系一定是（ ）
(A) 、异号 (B)
、同号 (C) >0， <0
(D) <0， >0
请将选择题答案写入表格：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
第Ⅱ部分 非选择题（共120分）
| 得分 | 评卷人 |
|
|
|
二、填空题（本大题共6小题，每小题3分，共18分．请把下列各题的正确答实填写在横线上）
11、已知
是反比例函数，则a=____ ．
12、在函数y=
+
中自变量x的取值范围是_________．
13、在反比例函数
的图象上有两点
和
，若
时，
，则的取值范围是 ．
14、.已知圆柱的侧面积是
，若圆柱底面半径为
，高为
，则与的函数关系式是
。
15、我们学习过反比例函数.例如,当矩形面积S一定时,长a是宽b 的反比例函数,其函数关系式可以写为a=
(S为常数,S≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例:______________________________________________________________;
函数关系式:_______________________
16、若A、B两点关于轴对称，且点A在双曲线
上，点B在直线
上，设点A的坐标为（a,b）,则
=
。
三、解答题(本大题共9小题，共102 分．解答应写出文字说明、证明过程或演算步骤)
| 得分 | 评卷人 |
|
|
|
17（9分）设函数y=（m-2）
，当m取何值时，它是反比例函数？它的图象位于哪些象限？求当≤x≤2时函数值y的变化范围．
|
| 得分 | 评卷人 |
|
|
|
18（9分）已知甲、乙两站的路程是312 km,一列列车从甲站开往乙站，设列车的平均速度为km/h，所需时间为h。
（1）试写出关于的函数关系式；
（2）2006年全国铁路第六次大提速前，这列列车从甲站到乙站需要4 h，列车提速后，速度提高了26 km/h，问提速后从甲站到乙站需要几个小时？
| 得分 | 评卷人 |
|
|
|
19（10分）已知一次函数y=x+m与反比例函数y=
(m≠-1)的图象在第一象限内的交点为P(x0,3).
(1)求x0的值;
(2)求一次函数和反比例函数的解析式.
| 得分 | 评卷人 |
|
|
|
| 座位号 |
|
|
20（10分）、已知函数
和
。
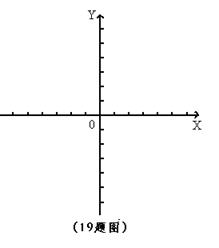
（1）在所给的19题图的坐标系中画出这两个函数的图象。
（2）求这两个函数图象的交点坐标。
（3）观察图象，当在什么范围时，
？
解： ：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 姓 名 |
|
|
| 得分 | 评卷人 |
|
|
|
| 班 级 |
|
|
21（12分）、已知正比例函数y＝4x，反比例函数y＝
．
求：（1）k为何值时，这两个函数的图象有两个交点？k为何值时，这两个函数的图象没有交点？
（2）这两个函数的图象能否只有一个交点？若有，求出这个交点坐标；若没有，请说明理由．
| 学 校 |
|
|
| 得分 | 评卷人 |
|
|
|
22（12分）、已知y=y1+y2 ,y1与ｘ＋1成正比例，ｙ2与ｘ＋1成反比例，当ｘ＝0时，ｙ＝－5；当ｘ＝2时，ｙ＝－7。
（1）求ｙ与ｘ的函数关系式；
（2）当ｙ＝5时，求ｘ的值。
| 得分 | 评卷人 |
|
|
|
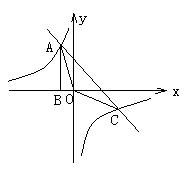
23（12分）、如图,Rt△ABO的顶点A是双曲线y=与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
 |
| 得分 | 评卷人 |
|
|
|
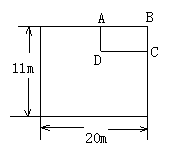
24（14分）某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m和11m的矩形大厅内修建一个60m2的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m2,新建(含装修)墙壁的费用为80元/m2.设健身房的高为3m,一面旧墙壁AB 的长为xm,修建健身房墙壁的总投入为y元.
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12, 当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
| 得分 | 评卷人 |
|
|
|
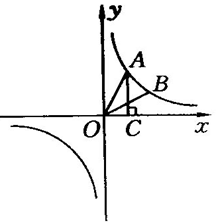
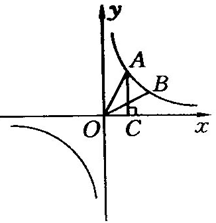
25（14分）、如图所示，点A、B在反比例函数y=的图象上，且点A、B的横坐标分别为a、2a（a>0），AC⊥x轴于点C，且△AOC的面积为2．
（1）求该反比例函数的解析式．
（2）若点（-a，y1）、（-2a，y2）在该函数的图象上，试比较y1与y2的大小．
（3）求△AOB的面积．
附答案：
一、选择题。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | B | C | A | C | B | D | D | A |
二、填空题。
11、
12、
13、
14、
15、（仅供参考）如：当路程s一定时,速度v是时间t的反比例函数;函数关系式为v=
(s是常数)
16、16
三、解答题。
17、解：依题意可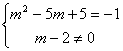得：
；解得：
∴当时，函数y=（m-2）是反比例函数；当时，代入可得：
；∵
，∴它的图象位于第一、第三象限。
由可得
，∵≤x≤2；∴
；解得：
。
18、解：（1）依题意可得：
；∴关于的函数关系式是
；
（2）把
代入可得：
；
∴提速后列车的速度为
；
当
时，
；
答：提速后从甲站到乙站需要3个小时。
19、解：(1)∵点P(x0,3)在一次函数y=x+m的图象上.
∴3=x0+m,即m=3-x0.
又点P(x0,3)在反比例函数y= 的图象上.
∴3=
,即m=3x0-1. ∴3-x0=3x0-1,解得x0=1.
(2)由(1),得m=3-x0=3-1=2, ∴一次函数的解析式为y=x+2,
反比例函数的解析式为y=
20、解：（1）函数的自变量取值范围是：全体实数，函数的自变量取值范围是：
，列表可得：
| x | … | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | … |
|
| … | -6 | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | 4 | … |
|
| … |
|
| -2 | -3 | -6 | 6 | 3 | 2 |
|
| … |
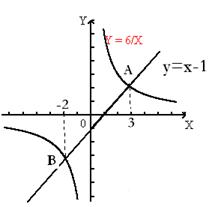
（2）联立解析式：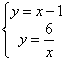
解得：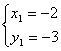
，
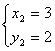
∴两函数的交点坐标分别为A（-2，-3）；B（3，2）；
（3）由图象观察可得：当
时，。
21、解：（1）联立解析式：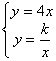
，可得：
，∵∴
；
若两个函数的图象有两个交点，则
，解得：
；
若两个函数的图象没有交点，则
，解得：
（2）∵
∴两个函数的图象不可能只有一个交点。
22、解：（1）设
，
；则有：
∵当ｘ＝0时，ｙ＝－5；当ｘ＝2时，ｙ＝－7；
∴有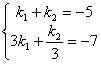
解得：
；
与的函数关系式为：
；
（2）把ｙ＝5代入可得：
解得：
。（检验：略）
23、解:(1)设A点坐标为(x,y),且x<0,y>0则
S△ABO=·│BO│·│BA│=·(-x)·y=。
∴xy=-3.
又∵y=,即xy=k,∴k=-3.
∴所求的两个函数的解析式分别为y=-,y=-x+2.
(2)由y=-x+2,令y=0,得x=2.
∴直线y=-x+2与x轴的交点D的坐标为(2,0).
再由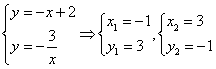
∴交点A为(-1,3),C为(3,-1).
∴S△AOC=S△ODA+S△ODC=
。
24、解:(1)根据题意,AB=x,AB·BC=60,所以BC=
。
y=20×3(x+)+80×3(x+)
即y=300(x+).
(2)把y=4 800代入y=300(x+)可得：4 800=300(x+).
整理得x2-16x+60=0.
解得x1=6,x2=10.
经检验,x1=6,x2=10都是原方程的根.
由8≤x≤12,只取x=10.
所以利用旧墙壁的总长度10+
=16m.
25、解：（1）∵A点在反比例函数
的图象上，∴设点A的坐标为A（，
），由
，得
，即
。
∴所求反比例函数的解析式为
。
（2）∵
，∴
。∵点（-a，y1）、（-2a，y2）在反比例函数的图象上，且都在第三象限的分支上，而该函数图象在第三象限随的增大而减小，
。
（3）作BD⊥轴，垂足为点D，
∵B点在反比例函数的图象上，∴B点的坐标为（
，
），
∴