| 座 号 |
|
|
八年级数学第二学期阶段考试试卷
| 题号 | 一 | 二 | 三 | 合计 | ||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得分 | ||||||||||||
（考查内容：第十八章 勾股定理 ）
说明：1、全卷共8页。考试时间90分钟，满分150分．
2、答卷前，考生必须将自己的座号、姓名、班级、学校按要求填写在密封线左边的空格内。
3、答题可用黑色钢笔、圆珠笔按各题要求答在试卷上，但不能用铅笔或红笔
| 姓 名 |
|
|
第Ⅰ部分 选择题（共30分）
| 得分 | 评卷人 |
|
|
|
一、选择题（本题共10小题，每小题3分，共30分．每小题给出的4 个选项中只有一个是符合题目要求的。）
1、在
中，∠C＝90°，
、
、
分别表示
、
、
的对边，则下列各式中，不正确的是（ ）
（A） 
（B）
（C）
（D） 
2、一直角三角形的一直角边长为6，斜边长比另一直角边长大2，则斜边的长为（ ）
| 班 级 |
|
|
（A） 4 （B） 8 （C） 10 （D） 12
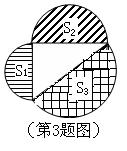3、如图所示，直角三边形三边上的半圆面积从小到大依次记为
、
、
，则、、的关系是（ ）
（A）
（B）
（C）
（D） 
4、若等边△ABC的边长为2cm，那么△ABC的面积为（ ）．
（A）
cm2
（B）
cm2 （C）
cm2 （D）4cm2
| 学 校 |
|
|
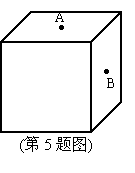
5、点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心，一只蚂蚁在盒子表面由A处向B处爬行，所走最短路程是（ ）
（A） 40 cm （B） 
cm （C） 20 cm （D）
cm
6、在下列以线段a、b、c的长为三边的三角形中，不能构成直角三角形的是 （ ）
（A）a=9 、b=41 、c=40 （B）a=11 、b=12 、c=15
（C）a∶b∶c=3∶4∶5
（D） a=b=5 、c=
7、在△ABC中，AB=12cm， BC=16cm， AC=20cm， 则△ABC的面积是( )
（A）96cm2 (B) 120cm2 (C) 160cm2 (D) 200cm2
8、锐角三角形的三边长分别是2、3、x，则x的取值范围是（ ）
（A）
<x<
（B）<x<5 （C）1<x< （D）1<x<5
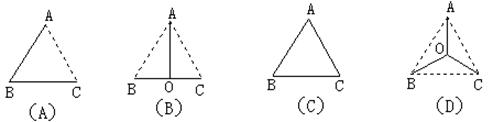9、已知如图，水厂A和工厂B、C正好构成等边△ABC，现由水厂A和B、C两厂供水，要在A、B、C间铺设输水管道，有如下四种设计方案，（图中实线为铺设管道路线），其中最合理的方案是（ ）
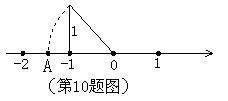10、如图，数轴上的点A所表示的数为x，则x2-10的立方根为（ ）
（A）
-10 （B） --10
（C） 8 （D） -12
请将选择题答案写入表格：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
第Ⅱ部分 非选择题（共120分）
| 得分 | 评卷人 |
|
|
|
二、填空题（本大题共6小题，每小题3分，共18分．请把下列各题的正确答实填写在横线上）
11、等腰△ABC的底边BC为16，底边上的高AD为6，则腰长AB的长为____________。
12、若正方形的面积为18cm2，则正方形对角线长为__________cm。
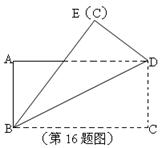13、如图所示，礐石某风景名胜区为了方便游人参观，从主峰A处架设了一条缆车线路到另一山峰C处，若在A处测得∠EAC=30°，两山峰的底部BD相距900米，则缆车线路AC的长为_______米．
（第13题图）
14、命题“全等三角形的面积相等”的逆命题是： ，
它是 （填入“真”或“假”）命题。
15、一个直角三角形的两边长分别为3cm和4cm,则第三边的长为 。
16、如图，矩形纸片ABCD，AB=2，
，沿对角线BD折叠（使
和
落在同一平面内），则A、E两点间的距离为 。
三、解答题(本大题共9小题，共102 分．解答应写出文字说明、证明过程或演算步骤)
| 得分 | 评卷人 |
|
|
|
17、（9分）在中，∠C＝90°，、、分别表示、、的对边（如图）。
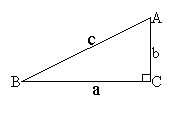⑴ 已知ｃ＝25，ｂ＝15，求ａ；
⑵ 已知ａ＝
，∠A＝60°，求ｂ、ｃ。
| 得分 | 评卷人 |
|
|
|
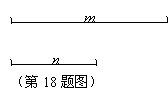
18、（9分）已知：线段
、
（
求作：线段
，使得
。（保留作图痕迹，不要求写作法和证明，但应在图中标示各线段的长并写明结论）
| 得分 | 评卷人 |
|
|
|
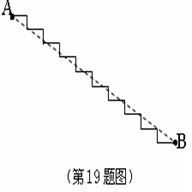
19、（10分）如图，一段楼梯，每级台阶的高度为30cm，宽度为36cm，A、B两点间相距多远？
| 得分 | 评卷人 |
|
|
|
| 座位号 |
|
|
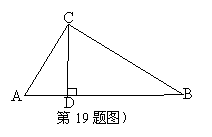
20、（10分）如图，
中，CD是AB边上的高，且
，求证：是直角三角形。
| 姓 名 |
|
|
| 得分 | 评卷人 |
|
|
|
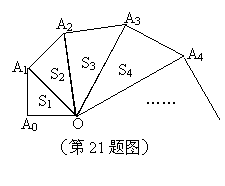
21、（12分）如图所示，螺旋形是由一系列直角三角形组成，其中
，
表示第个三角形的面积。
（1）请你用的代数式表示。
（2）求
的值。
| 班 级 |
|
|
| 学 校 |
|
|
| 得分 | 评卷人 |
|
|
|
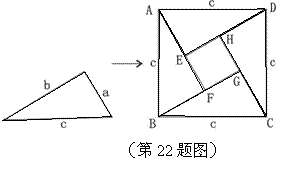
22、（12分）如图所示，用四个边长是a，b，c的直角三角形拼成右边的一个正方形，用这种拼图，你能推导出勾股定理吗？写出你的推导过程。
| 得分 | 评卷人 |
|
|
|
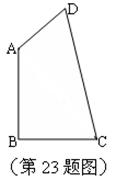23、（12分）如图所示，在四边形ABCD中，已知：
，且
，求
的度数。
| 得分 | 评卷人 |
|
|
|
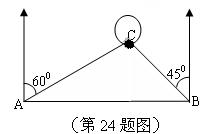
24、（14分）如图，北海海面上，一艘解放军军舰正在基地A的正东方向且距A地40海里的B处训练，突然接基地命令，要该舰前住C岛，接送一病危渔民到基地医院救治，已知C岛在A的北偏东
方向，且在B北偏西
方向，军舰从B处出发，平均每小时走20海里，需要多少时间才能把患病渔民送到基地医院？（精确到0.1小时，参考数据：
）
| 得分 | 评卷人 |
|
|
|
25、（14分）已知：矩形ABCD（四个角都是直角）。
（1）如图25—（1），P为矩形ABCD的边AD上一点，求证：
。
（2）如图25—（2），当点P运动到矩形ABCD外时，结论是否仍然成立？请说明你的理由。
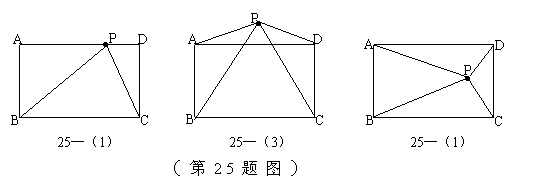（3）如图25—（3），当点P运运到矩形ABCD内时，结论是否仍然成立呢？请说明你的理由。