菱形
快速反应
1. ______________的平行四边形叫做菱形。
2.
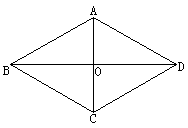如图，在菱形ABCD中，对角线AC、BD相交于点O,则
⑴ AB=AD=_______=_______,即菱形的_______________相等
⑵
图中的等腰三角形有__________________,直角三角形有_________________,△AOD≌____________≌____________≌_____________，由此可以得出菱形的对角线__________________,每一条对角线________________.
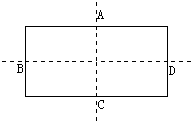
3. 菱形是轴对称图形，它的对称轴是_____________
4. 按图示的虚线折纸，然后连接ABCD可得菱形，由此可以得到_____________的四边形是菱形。
5. 木工做菱形窗棂时总要保持四条边框一样长，道理是_____________
6.
如图，平行四边形ABCD的两条对角线AC、 BD相交于点O，AB=
,AO=1,OB=2,则AC、BD的位置关系是________________,四边形ABCD是菱形的道理是________
自主学习
1． 菱形的周长为20 cm，两邻角的比为1:2，则较短对角线的长是_____________;一组对边的距离是____________.
2． 已知菱形的对角线长分别为12m和16m，求菱形的高。
3．
如图，两条等宽的长纸条倾斜地重叠着，试证重叠部分ABCD为菱形。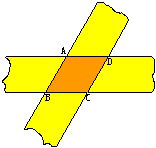
4．
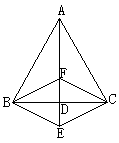如图，△ABC中，AB=AC，AD是角平分线，E为AD延长线上一点，CF//BE交AD于F，连接BF、CE，求证：四边形BECF是菱形。
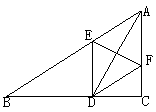
5． 如图，△ABC中，∠C=90°，AD平分∠BAC，ED⊥BC，DF//AB，求证：AD与EF互相垂直平分。
6． 作菱形ABCD，使AC＝5cm，∠BAD＝60°．
7．
四边形ABCD中，AB=BC=CD=DA，∠BAD=120°,M为BC上的点，若△AMN有一角等于60°，求证：△AMN为等边三角形。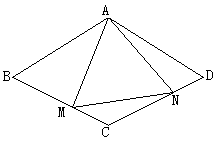
8． 如图，菱形ABCD的对角线AC与BD相交于O，∠ABC≠90°，则图中的全等三角形共有（ ）
A.42对 B.6对 C.8对 D.12对
1． 填空：
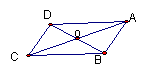
（1）如图，在菱形ABCD中，AB=5,OA=4,OB=3,则菱形的周长是
两条对角线的长是 ；
（2）菱形的两条对角线的长分别是6厘米和8厘米，那么菱形的面积是 ；
（3）菱形的一条对角线与一条边长相等，则菱形相邻两个内角的度数分别为
；
2．如图，在菱形ABCD中，∠BAD=2∠B,是说明△ABC等边三角形
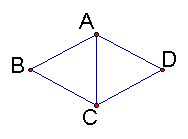
3．已知菱形ABCD中，AC与BD相交O点，若∠BDC =
,菱形的周长为20厘米，求最短对角线长
引导学生画出图形，进行分析。
分析：由菱形的条件，我们可以知道AC、BD分别平分两组对角,AB=BC=CD=AD，可知∠ADC等于2倍的∠BDC，知道∠BDC =，所以∠ADC是60º，知△ACD等边三角形，问题就可解决。
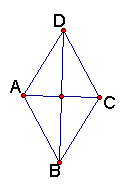
小结： 菱形是特殊的平行四边形，它有什么性质？
边：对边平行；邻边相等；四条边都相等．
角：对角相等、邻角互外．
对角线：对角线互相平分，互相垂直，每条对角线平分一组对角，
菱形常用的判定方法：
1．一组邻边相等的平行四边形．
2．四条边相等的四边形．
3．对角线互相垂直的平行四边形．
课后作业：《畅游数学》第四章第3节
四、作业
1．已知菱形的两条对角线长分别是6cm和8cm．求菱形的周长和面积．
2．已知菱形的周长为20cm，两个相邻的角的度数的比为1∶2，求较长的对角线长．
3．求证：菱形对角线交点到各边距离相等．
4．求证：有一条对角线平分一个内角的平行四边形是菱形．
5．在
ABCD中，∠A的平分线与BC边相交于点E，∠B的平分线与AD边相交于点F．求证：四边形ABEF是菱形．
6．作菱形ABCD，使AC＝5cm，∠BAD＝60°．
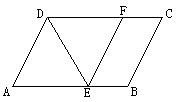
9． 如图，DE是□ABCD中∠ADC的平分线，EF//AD交DC于F.
(1) 求证：四边形AEFD是菱形。
(2) 如果∠A=60°，AD=5,求菱形AEFD的面积。
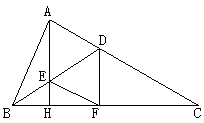
如图，△ABC中，∠A=90°, ∠B的平分线交AC于D，AH、DF都垂直于BC，H、F为垂足，求证：四边形AEFD为菱形。