解直角三角形单元测试卷
113中 钟添琼
一、填空题：（每题2分，共20分）
1.若锐角α、β互余且cosα＝4/5，则sinβ＝________，cosβ＝__________。
2.在直角三角形ABC中，
C＝60°，斜边BC＝14 cm，则BC边上的高为__________
cm 。
3.等边三角形的面积为
，则边长为
,高为_________.
4.Rt△ABC中，∠C＝90°，CD⊥AB于D，sinB＝3/4，则
∠DCA＝__________
5.锐角α满足sinα＝cos38°16′，则α＝__________。
6. 三角形的一锐角A满足关系式
，则A＝
.
7.三角形三边为3，7，
，则最大锐角的余弦值为__________。
8..直角三角形的周长为24cm，一个锐角的正弦值为3/5，则面积为__________。
9.等腰梯形ABCD中，AB∥DC，AD＝BC，若∠D=105°，对角线AC⊥BD,
则tan∠DAC= .
10. 已知α为锐角，且
，则α=
.
二、选择：（每题3分，共30分）
11、已知：α为锐角，且
，那么下列各式中正确的是（ ）
A.
B.
C. 
D. 
12.在锐角
中,已知
,且AB=4,则的面积等于（ ）
A.4 B.
C. 
D. 2
13、已知等腰三角形顶角为120°，底上的高为5，则一腰上的高为（ ）
（a）5 （b）5
（c）5
（d）10
14、下列各式正确的是（ ）
（a）sin20°＋sin20°＝sin40° （b）
31°＝（90°－59°）
（c）sin2A＋cos2（90°－A）＝1 （D）sin
＝cos
（其中A+B+C＝180°）
15. Rt△ABC中,∠C=90°,D为BC上一点，∠DAC=30°，BD＝2，AB＝2，则AC的长是（ ）
A.
B.2
C.3
D.
16. 上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处，从A、B两处分别测得小岛M在北偏东45°和北偏东15°方向，则在B处船与小岛M的距离是（ ）
A.20海里
B.20海里
C.15海里
D.20
17. 
为锐角，则
（ ）
A. 
B. 
C. 0 D.
18.在
中, 
,
, AD平分
交BC于D,则
（ ）
A. 1：2 B. 
C. 2：3 D. 
19.在中, ,如果AB=c, BC=a,且a、c满足
,则
（ ）
A. 1 B. 
C. 1或
D. 1或3
20.若
,且
, 则
等于（ ）
A. 
B. 
C. 
D. 
三、解答题:
21.（5分）计算 cos245°+sin60°·30°－
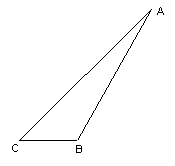
22.（7分）如图，三角形△abc中，∠b＝45°，∠c＝60°，ab＝
，ad⊥bc于d，
求cd
23.（7分）如图，已知四边形ABCD中，BC＝CD＝DB，∠ADB=90°，cos∠ABD=4/5,
求S△ABD:S△BCD.
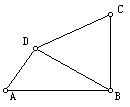
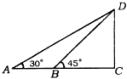
24.（7分）如图，在上海黄埔江东岸，矗立着亚洲第一的电视塔“东方明珠”，某校学生在浦江西岸B处，测得塔尖D的仰角为 
，后退340米到A点测得塔尖D仰角为 
，设塔底C与B、A在一直线上，试求该塔的高度（精确到1米）。
25.（8分）已知中,AB=AC,CH是AB边上的高,且
,求
的
值和CH的长.
26.（8分）在△abc中，∠c＝90°，若b＋c＝90，∠a－∠b＝30°，解这个直角三角形。
27.（8分）在中，
求
.
