八年级数学说说旋转变化练习题

说说旋转变换

胡明华

　　将平面图形F₁绕定点M旋转一个定角a，得到图形F₂，这就是旋转变换。在旋转变换下，旋转前后的图形全等。旋转变换多用在等腰三角形、正三角形、正方形等较规则的图形上。

  1. 旋转后，使分散的条件相对集中，便于问题的解决

　　例1. 如图1，为边的是等边三角形，求AP的最大、最小值。

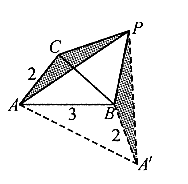
图1

　　分析：已知条件AB=3，AC=2与所求的AP比较分散。考虑到是等边三角形，若绕点P逆时针旋转到，则

　　可得是等边三角形，，则与所求就集中到中（特殊情况A，，B三点在同一直线）。

　　由于，

　　所以。

　　即　AP的最大值为5，最小值为1。

  2. 由条件和结论出发，确定旋转的方向、角度

　　例2. 已知：正方形ABCD内一点E到A、B、C三点的距离之和的最小值为，求此正方形的边长。

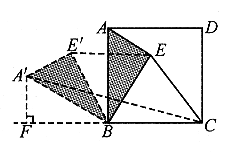
图2

　　分析：已知条件EA+EB+EC的最小值为，由于EA、EB、EC比较分散，不便解决。可将绕点B逆时针旋转得。为什么要旋转呢？因旋转是等边三角形，

，就转化为一条折线的长，进一步，而是定长。故当E落在上（显然此时）时，的最小值，因而

　　

　　下面只要作，得

　　

　　请看应用

　　例3. 已知：，求证：

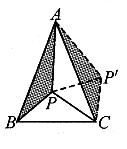
图3

　　分析：绕点A旋转至，如图3连结则

　　

　　

　　例4. 如图4，在四边形ABCD中，AB=BC，，K为AB上一点，N为BC上一点。若的周长等于AB的2倍，求的度数。

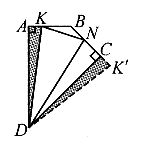
图4

　　分析：显然，绕点D顺时针方向旋转至

　　

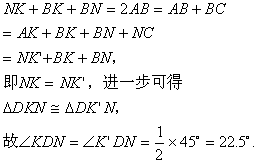
　　例5. 如图5，⊙⊙及定点P，定角⊙上点C，⊙上点D，使PC=PD，且。

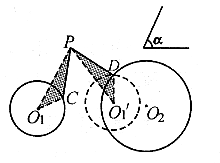
图5

　　分析：假设C、D两点已作出，把⊙绕点P逆时针旋转，到⊙，则旋转到的位置，显然，D就是⊙与⊙的交点。故本题可先连结，再以⊙的半径作⊙，交⊙于D，最后以P为圆心，以PD为半径作圆，交⊙于点C，可完成作图。

　　练习：

  1. 如图6，正方形ABCD内一点P，PA：PB：PC=1：2：3，求

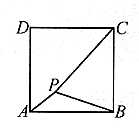
图6

  2. 如图7，分别在AB、BC、AC上，求证（提示：可将）。

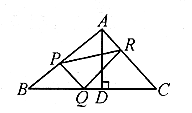
图7

  3. 如图8，三角形互相平行，，C在直线n上，且使为一等边三角形。（提示：作逆时针旋转）

图8

年级

初中

学科

数学

版本

期数

内容标题

说说旋转变换

分类索引号

G.622.46

分类索引描述

辅导与自学

主题词

说说旋转变换

栏目名称

中考经典

供稿老师

审稿老师

录入

韩素果

一校

康纪云

二校

审核