9月20日 平行四边形的判别1
快速反应
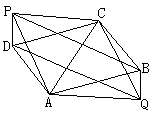
1. 如图，四边形ABCD，AC、BD相交于点O,若OA=OC,OB=OD,则四边形ABCD是___________,根据是______________
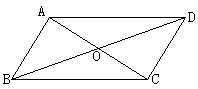
2. 如图，四边形ABCD中，AB//CD,且AB=CD,则四边形ABCD是______________,理由是_______________
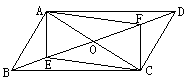
3. 如图，在□ABCD中，AC、BD相交于点O,E、F分别在OB、OD上，且OE=OF,又OC=__________,所以__________是平行四边形，理由是_____________
4. 用两个全等的三角形按不同的方法拼成四边形，在这些四边形中，平行四边形的个数是（ ）
A.1个 B.2个 C.3个 D.4个
5. 判断：一条对角线平分另一条对角线的四边形是平行四边形（ ）
自主探索
i. 如图，□ABCD中，AE、CF分别与直线DB 相交于E和F,且AE//CF, 求证：CE//AF.
ii. 如图，□ABCD中，BM垂直AC于M,DN垂直AC于N, 求证：四边形BMDN是平行四边形。
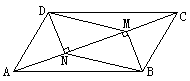
iii. 如图，□ABCD中，点M、N是对角线AC上的点，且AM=CN,DE=BF,求证：四边形MFNE是平行四边形。
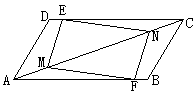
iv. 如图，AB、CD相交于点O,AC//DB,AO=BO,E、F分别为OC、OD的中点，连接AF、BE,求证：AF//BE.
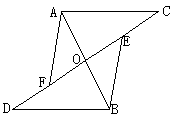
v.
在四边形ABCD中，AB//CD,对角线AC、BD交于点O，EF过O交AB于E，交CD于F，且OE=OF，求证，ABCD是平行四边形。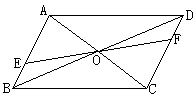
vi.
如图，过□ABCD对角线的交点O作直线EF交AD、BC分别于E、F，又G、H分别为OB、OD的中点，求证：四边形EHFG为平行四边形。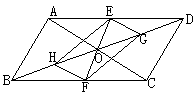
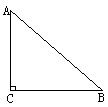
vii. 现有一块等腰直角三角形的铁板，通过切割焊接成一个含有45°角的平行四边形，请你设计一种最简单的方案，并证明你的方案得到的是一个符合平行四边形的四边形。
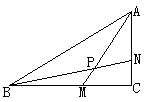
viii. 如图，在△ABC中，∠C=90°，点M在BC上，且BM=AC，点N在AC上，且AN=MC。AM与BN相交于点P。求证：∠BPM=45.
9月21日 平行四边形的判别2
快速反应
6. 如图，四边形ABCD为平行四边形，AB=6,BC=8,则AD=_______,CD=________,根据是__________
7.
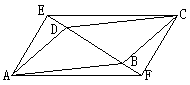
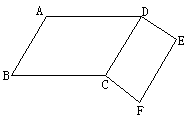
如图，AB
DC=EF=10, DE=CF=8,则图中的平行四边形有__________,理由分别是_______________、__________________
8. 下列说法，属于平行四边形判别方法的有（ ）个
①两组对边分别平行的四边形；
②平行四边形的对角线互相平分；
③两组对边分别相等的四边形；
④平行四边形的每组对边平行且相等；
⑤两条对角线互相平分的四边形是平行四边形；
⑥一组对边平行且相等的四边形是平行四边形。
A.6个 B.5个 C.4个 D.3个
自主探索
1． 如图，在□ABCD中，E、F、G、H分别是四条边上的点，且满足BE=DF,CG=AH,连接EF、GH。求证：EF与GH互相平分。
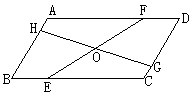
2． 如图，以△ABC的三条边为边向BC的同一侧作等边△ABP、等边△ACQ，等边△BCR，求证：四边形PAQR为平行四边形。
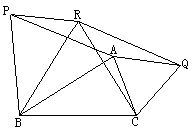
3． 如图，在△ABC中，∠C=90°，点M在BC上，且BM=AC，点N在AC上，且AN=MC。AM与BN相交于点P。求证：∠BPM=45°
4． △ABC的三条中线分别为AD、BE、CF，H为BC边外一点，且BHCF为平行四边形，求证：AD//EH.
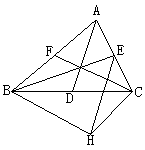
5． 已知：线段a、b、c，求作□ABCD，使BC=a，对角线AC=b，BD=c.
6． 如图，已知AC是□ABCD的对角线，△ACP和△ACQ都是等边三角形，求证：四边形BPDQ是平行四边形。
