第二章 分解因式综合练习
一、选择题
1.下列各式中从左到右的变形，是因式分解的是（ ）
(A)(a+3)(a-3)=a2-9 (B)x2+x-5=(x-2)(x+3)+1
(C)a2b+ab2=ab(a+b) (D)x2+1=x(x+
)
2.下列各式的因式分解中正确的是（ ）
(A)-a2+ab-ac= -a(a+b-c) (B)9xyz-6x2y2=3xyz(3-2xy)
(C)3a2x-6bx+3x=3x(a2-2b) (D)
xy2+x2y=xy(x+y)
3.把多项式m2(a-2)+m(2-a)分解因式等于（ ）
(A)(a-2)(m2+m) (B)(a-2)(m2-m) (C)m(a-2)(m-1) (D)m(a-2)(m+1)
4.下列多项式能分解因式的是（ ）
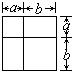
(A)x2-y (B)x2+1 (C)x2+y+y2 (D)x2-4x+4
5.下列多项式中，不能用完全平方公式分解因式的是（ ）
(A)
(B)
(C)
(D)
6.多项式4x2+1加上一个单项式后，使它能成为一个整式的完全平方，则加上的单项式不可以是（ ）
(A)4x (B)-4x (C)4x4 (D)-4x4
7.下列分解因式错误的是（ ）
(A)15a2+5a=5a(3a+1) (B)-x2-y2= -(x2-y2)= -(x+y)(x-y)
(C)k(x+y)+x+y=(k+1)(x+y) (D)a3-2a2+a=a(a-1)2
8.下列多项式中不能用平方差公式分解的是（ ）
(A)-a2+b2 (B)-x2-y2 (C)49x2y2-z2 (D)16m4-25n2p2
9.下列多项式：①16x5-x；②(x-1)2-4(x-1)+4；③(x+1)4-4x(x+1)+4x2；④-4x2-1+4x，分解因式后，结果含有相同因式的是（ ）
(A)①② (B)②④ (C)③④ (D)②③
10.两个连续的奇数的平方差总可以被 k整除，则k等于（ ）
(A)4 (B)8 (C)4或-4 (D)8的倍数
二、填空题
11.分解因式：m3-4m= .
12.已知x+y=6，xy=4，则x2y+xy2的值为 .
13.将xn-yn分解因式的结果为(x2+y2)(x+y)(x-y)，则n的值为 .
14.若ax2+24x+b=(mx-3)2，则a= ，b= ，m= . (第15题图)
15.观察图形，根据图形面积的关系，不需要连其他的线，便可以得到一个用来分解因式的公式，这个公式是 .
三、(每小题6分，共24分)
16.分解因式：(1)-4x3+16x2-26x
(2)a2(x-2a)2-
a(2a-x)3
（3）56x3yz+14x2y2z－21xy2z2 (4)mn(m－n)－m(n－m)
17.分解因式：(1) 4xy–(x2-4y2) (2)-(2a-b)2+4(a -b)2
18.分解因式：(1)-3ma3+6ma2-12ma (2) a2(x-y)+b2(y-x)
19、分解因式
（1）
； （2）
；
（3）
；
20.分解因式：(1)ax2y2+2axy+2a (2)(x2-6x)2+18(x2-6x)+81 (3) –2x2n-4xn
21．将下列各式分解因式：
（1）
； （2）
； （3）
；
22．分解因式（1）
；
（2）
；
23.用简便方法计算：
(1)57.6×1.6+28.8×36.8-14.4×80 (2)39×37-13×34
（3）．13.7
24．试说明：两个连续奇数的平方差是这两个连续奇数和的2倍。
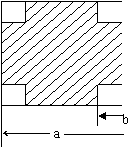
25．如图，在一块边长为a厘米的正方形纸板四角，各剪去一个边长为 b(b<
)厘米的正方形，利用因式分解计算当a=13.2，b=3.4时，剩余部分的面积。
 |
26．将下列各式分解因式
（1）
（2）
；
(3)
(4)
(5)
(6)
(7)
(8)
(9)
（10）(x2+y2)2-4x2y2
（12）．x6n+2+2x3n+2+x2 （13）．9(a+1)2(a-1)2-6(a2-1)(b2-1)+(b+1)2(b-1)2
27.已知(4x-2y-1)2+
=0，求4x2y-4x2y2+xy2的值.
28．已知：a=10000，b=9999，求a2+b2－2ab－6a+6b+9的值。
29．证明58-1解被20∽30之间的两个整数整除
30.写一个多项式，再把它分解因式(要求：多项式含有字母m和n，系数、次数不限，并能先用提取公因式法再用公式法分解).
31.观察下列各式：
12+(1×2)2+22=9=32
22+(2×3)2+32=49=72
32+(3×4)2+42=169=132
……
你发现了什么规律？请用含有n(n为正整数)的等式表示出来，并说明其中的道理.
32.阅读下列因式分解的过程，再回答所提出的问题：
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是 ，共应用了 次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004，则需应用上述方法 次，结果是 .
(3)分解因式：1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).
34．若a、b、c为△ABC的三边，且满足a2+b2+c2－ab－bc－ca=0。探索△ABC的形状，并说明理由。
35．阅读下列计算过程：
99×99+199=992+2×99+1=（99+1）2=100 2=10 4
1．计算：
999×999+1999=____________=_______________=_____________=_____________；
9999×9999+19999=__________=_______________=______________=_______________。
2．猜想×+等于多少？写出计算过程。
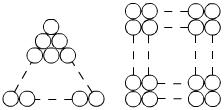36.有若干个大小相同的小球一个挨一个摆放，刚好摆成一个等边三角形(如图1)；将这些小球换一种摆法，仍一个挨一个摆放，又刚好摆成一个正方形(如图2).试问：这种小球最少有多少个？
图1 图2