18.2 勾股定理的逆定理（1）
知识领航
1．勾股定理的逆定理：如果三角形的三边长a、b、c满足a2＋b2＝c2，那么这个三角形是直角三角形．
2. 满足a2 +b2=c2的三个正整数，称为勾股数．勾股数扩大相同倍数后，仍为勾股数．常用的勾股数有3、4、5、；6、8、10；5、12、13等.
3. 应用勾股定理的逆定理时，先计算较小两边的平方和再把它和最大边的平方比较.
4. 判定一个直角三角形，除了可根据定义去证明它有一个直角外，还可以采用勾股定理的逆定理，即去证明三角形两条较短边的平方和等于较长边的平方，这是代数方法在几何中的应用.
e线聚焦
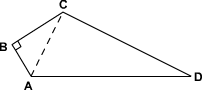
【例】如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积.
分析：根据题目所给数据特征，联想勾股数，连接AC，可实现四边形向三角形转化，并运用勾股定理的逆定理可判定△ACD是直角三角形.
解：连接AC，在Rt△ABC中，
AC2=AB2＋BC2=32＋42=25， ∴ AC=5.
在△ACD中，∵ AC2＋CD2=25＋122=169，
而 AB2=132=169，
∴ AC2＋CD2=AB2，∴ ∠ACD=90°．
故S四边形ABCD=S△ABC＋S△ACD=
AB·BC＋AC·CD=×3×4＋×5×12=6＋30=36.
双基淘宝
u 仔细读题，一定要选择最佳答案哟！
1. 分别以下列四组数为一个三角形的边长：（1）3，4，5；（2）5，12，13；（3）8，15，17；（4）4，5，6.其中能构成直角三角形的有（ ）
A.4组 B.3组 C.2组 D.1组
2. 三角形的三边长分别为 a2＋b2、2ab、a2－b2（a、b都是正整数），则这个三角形是（）
A．直角三角形 B．钝角三角形 C．锐角三角形 D．不能确定
3．如果把直角三角形的两条直角边同时扩大到原来的2倍，那么斜边扩大到原来的( )
A.1倍 B. 2倍 C. 3倍 D. 4倍
4. 下列各命题的逆命题不成立的是( )
A.两直线平行,同旁内角互补 B.若两个数的绝对值相等,则这两个数也相等
C.对顶角相等 D.如果a=b,那么a2=b2
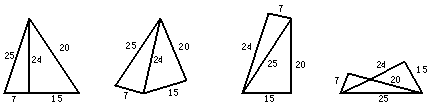
5．五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ）
A B C D
综合运用
u 认真解答，一定要细心哟！
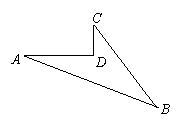6. 如图所示的一块地，已知AD=4m，CD=3m， AD⊥DC，AB=13m，BC=12m，求这块地的面积.
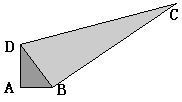
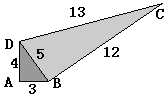
7. 一个零件的形状如左图所示，按规定这个零件中∠A和∠DBC都应为直角．工人师傅量得这个零件各边尺寸如右图所示，这个零件符合要求吗？
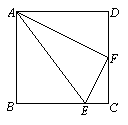8. 如图，E、F分别是正方形ABCD中BC和CD边上的点，且AB=4，CE=
BC，F为CD的中点，连接AF、AE，问△AEF是什么三角形？请说明理由.
拓广创新
u 试一试，你一定能成功哟！
9. 勾股数又称商高数，它有无数组，是有一定规律的.比如有一组求勾股数的式子：a=m2-n2,b=2mn,c=m2+n2（其中m，n为正整数，且m＞n）.你能验证它吗？利用这组式子，完成下表，通过表格，你会发现勾股数有哪些规律？请查阅有关资料，相信你将有更多收获.
|
| 1 | 2 | 3 | 4 | 5 | 6 | … |
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| … | … | … | … | … | … | … | … |
