八年级数学第一学期五校联考试卷
| 题号 | 一 | 二 | 三 | 四 |
| 得分 |
|
|
|
|
一、精心选一选（每小题3分，共30分。）
1．已知函数y=3x+1，当自变量增加3时，相应的函数值增加( ).
A．10 B．9 C．3 D．8
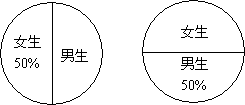
2．如下图,甲校女生占全校总人数的50%,乙校男生占全校总人数的50%,比较两校女生人数( ).
A．甲校乙校一样多 B．甲校多于乙数
C．甲校少于乙校 D． 不能确定
3．函数
中，自变量x的取值范围是（ ）
A．x≥－1 B．x＞0 C．x≥－1且x≠0 D．x＞－1且x≠0
4．若直线
：y＝kx＋b与直线y＝2x平行且经过点(2，－1)，则直线的解析式为
．
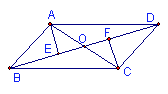
5．如图所示，已知AB∥CD，AD∥BC，AC与BD交于点O，AE⊥BD于E，CF⊥BD于E，图中全等三角形有（ ）
A．3对 B．5对 C．6 对 D．7对
6．在某扇形统计图中，其中某一部分扇形面积所对的圆心角是
，那么它所代表的部分占总体的（ ）
A．
B．
C．
D．
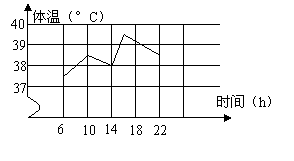
7．如图是护士为一名病人测量体温后绘制的折线图，
这位病人中午12时的的体温约为（ ）
A．39.2° B．38.5°
C．38.2° D．37.8°
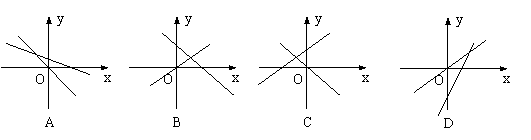
8．下列图形中，表示一次函数y = mx + n与正比例函数
y = mnx（m、n为常数，且mn≠0）的图象的是 （ ）
 |
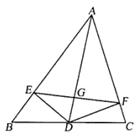5．如图，AD是△ABC是角平分线，DE⊥AB于点E，DE⊥AC于点F，连结EF交AD于点G，则AD与EF的关系是____________
10．中央电视台在今年六月份某一天发布的天气预报显示我国内地31个直辖市和省会城市的最高气温（0C）情况如下表：
| 气温（0C） | 18 | 21 | 22 | 23 | 24 | 25 | 27 | 28 | 29 | 30 | 32 | 33 | 35 | 36 |
| 城市数 | 1 | 1 | 1 | 3 | 1 | 3 | 1 | 5 | 4 | 3 | 1 | 4 | 1 | 2 |
那么能够显示这些城市在这一天数据的分布情况，可绘制（ ）
A．条形图 B．扇形图 C．折线图 D．直方图
二、耐心填一填（每小题3分，共30分）
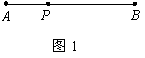1．已知，如图1，一轮船在离A港10千米的P地出发向B港匀速前进，30分钟后离A港26千米（未到达B港）．设出发x小时后，轮船离A港y千米（未到达B港），则y与x之间的函数关系是______．
2．弹簧挂上物体后会伸长，测得一弹簧的长度y(cm)与所挂物体的重量x(kg)有关系：
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| y | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
8
那么弹簧总长y(cm)与所挂物体质量x(kg)之间的函数关系式为 ．
3．直线
可由直线
向
平移 得到．
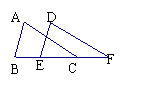
4．如图，已知∠ABC=∠DEF，AB=DE，要说明△ABC≌△DEF若以“SAS”为依据，还要添加的条件为______________．
5．已知一次函数
，函数
的值随
值的增大而增大，则
的取值范围是 ．
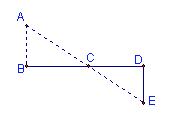
6．如图所示：要测量河岸相对的两点A、B之间的距离，先从B处出发与AB成90°角方向，向前走50米到C处立一根标杆，然后方向不变继续朝前走50米到D处，在D处转90°沿DE方向再走17米，到达E处，使A、C与E在同一直线上，那么测得A、B的距离为_____米．
7．把一组64个数据的样本分成8组，从第一组到第四组的频数分别为5、7、11、13，第五组到第七组的频率都是0.125，则第八组的频率为 ．
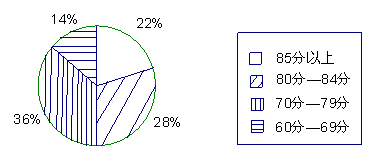
8．如图是某校九年级一班50名学生的一次数学测验成绩的扇形统计图，按图中划分的分数段，这次测验成绩中所占百分比最大的分数段是_________________．
9．点A(2，4)在正比例函数的图象上，这个正比例函数的解析式是 ．
10．已知直线
与轴,轴围成一个三角形,则这个三角形面积为 (平方单位)．
三、认真答一答（只要你认真思考, 仔细运算, 一定会解答正确的!）
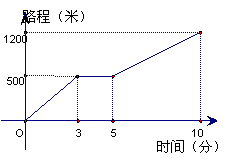
1．（8分）如图是小陈同学骑自行车上学的路程与时间的关系图，请你根据图像描述他上学路上的情况．
 |
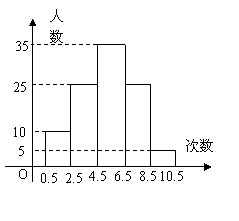2、（10分）为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图（如图），图中从左到右依次为第1、2、3、4、5组．
（1） 求抽取多少名学生参加测试？
（2） 处于哪个次数段的学生数最多？（答出是第几组即可）
（3） 若次数在5次（含5次）以上为达标，
求这次测试的达标率．
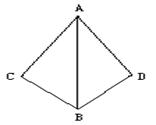3、（8分）已知：AB平分∠CAD，AC=AD．求证：BC=BD．
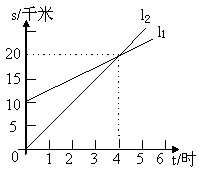4、（10分）如图，
反映了甲离开A的时间与离A地的距离的关系，
反映了乙离开A地的时间与离A地的距离之间的关系，根据图象填空：
（1）当时间为2小时时，甲离A地 千米，
乙离A地 千米。
（2）当时间为6小时时，甲离A地 千米，
乙离A地 千米．
（3）当时间 时，甲、乙两人离A地距离相等。
（4）当时间 时，甲在乙的前面，
当时间 时，乙超过了甲．
（5）对应的函数表达式为
，对应的函数表达式为 ．
5、（12分）（1）已知△ABC中， AE为角平分线，D为AE上一点，且∠BDE=∠CDE，
求证：AB=AC
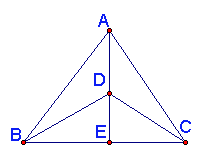（2）若把（1）中“AE角平分线”换为“AE为高线”，其它条件不变，结论还会成立吗？如果成立，请说明；若不成，也请说明理由．
6．（12分）不同年龄段的人每人每天膳食中钙的供给量标准如下：
3岁以下：600毫克 3~10岁：800毫克
10~13岁：1000毫克 13~16岁：1200毫克
16~18岁：1000毫克 18岁以上800毫克
（1）请你选择恰当的统计图把它们直观地表示出来．
（2）从统计图中你能获得什么信息？（请写出其中的两条信息）
（3）请你填写自己的年龄是 岁，并根据本题提供的数据，判断一下你每天膳食中应摄取 毫克的钙．
参考答案：
一、1、B 2、D 3、C 4、C 5、D 6、B 7、C 8、A 9、D 10、D
二、1. 
2. 
3、向下
2个单位 4、BE=CF或BC=EF
5、m>－2 6、17 7、0.025 8、70分～79分 9、y=2x 10、18
三、1、略 2、（1）100人（2）第3组最多（3）65% 3、利用△ACB≌△ADB（SAS）可得 4、（1）15 10 （2）25 30 （3）等于4；（4）小于4；大于4 （5）y1=2. 5 x+10,
y2=5x 5、（1）先说明∠ADB=∠ADC，利用△ADB≌△ADC（ASA） （2）先利用△DBE≌△DCE（ASA）得出BD=CD，再说明△ADB≌△ADC（SAS）可得．6、略