八年级数学
第一学期期中考试试卷
注意：答案做在答题卡上，只交答题卡，试卷不交。
一、 选择题：(每题3分，共36分)
1、 在
中，无理数有（ ）
A、1个 B、2个 C、3个 D、4个
2、一根木桩在地上影长等于木桩实际长4，这木桩顶端到影子顶端的距离为 （ ）
A、
B、
C、
D、
3、下列说法不正确的（ ）
A、
；B、
；
C、
的算术平方根是4 ；D、
4、正方形具有而菱形不一定具有的性质是 （ ）
A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线平分一组对角
5、已知直角三角形的两条直角边分别为6cm和8cm，那么斜边上的高为
（ ）
A、10 B、2.4 C、4.8 D、24
6、经过旋转作图可能得到图形
的是 （ ）
7．下列美丽的图案，既是轴对称图形又是中心对称图形的个数是 （ ）
 |
A．1个 B．2个 C．3个 D．4个
8．一个正多边形,它的一个外角等于与它相邻的内角的
,则这个多边形是（ ）
A．正十二边形 B．正十边形 C．正八边形 D．正六边形
9．如图，□ABCD的周长为16cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为 ( )
A．4 cm B．6cm C．8cm D．10cm
10．若菱形的边长为1cm，其中一内角为60°，则它的面积为 （ ）
A ．
B．
C．
D．
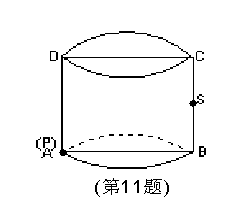
11．如图，圆柱的轴截面ABCD是边长为4的正方形，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离是 （ ）
A．
B．
C．
D．
12、如图x在数轴上表示数的点的位置，则化简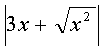
的结果是（ ）
A．-4x
B．4x C．-2x
D．2x
 |
X 0
第12题
二、 耐心填一填：（每小题3分，计33分）
13．有一块边长为24米的正方形绿地，如图所示，在绿地旁边B处有健身器材，由于居住在A处的居民践踏了绿地，小明想在A处树立一个标牌“少走▇米，踏之何忍？”请你计算后帮小明在标牌的▇填上适当的数字为：
。
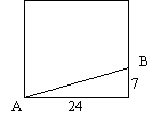
第13题 第14题 第15题
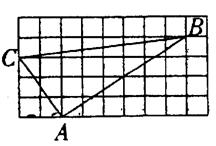
14.如图，正方形网格中的△ABC，若小方格边长都为1，则△ABC是： 三角形。
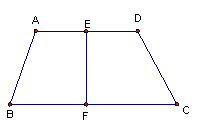
15. 如图，在梯形ABCD中，AD∥BC，∠B ＋∠C ＝900，AD＝1，BC ＝3，E、F分别是AD、BC的中点，则EF＝ .
16.已知四边形ABCD中，AD∥BC，要使四边形为平行四边形，还需要添加条件____________(只须填写一个你认为正确的即可)
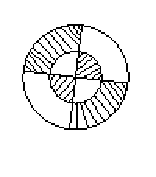
17．如图，是两个同心圆，其中两条直径互相垂直，其大圆的半径是2，则其阴影部分的面积之和 ．（结果保留π）
 | |||
 | |||
第17题 第18题
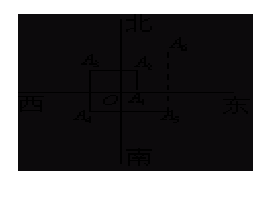
18．如图，一个机器人从O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2点，再向正西方向走9米到达A3点，再向正南方向走12米到达A4点，再向正东方向走15米到达A5点。按如此规律走下去，当机器人走到A6点时，离O点的距离是 米
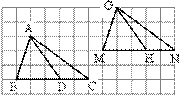19、如图，
的位置，BC上一点D也同时平移到点H的位置，若
20、化简：
21．观察下列各式：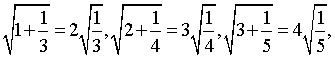
……请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是_________
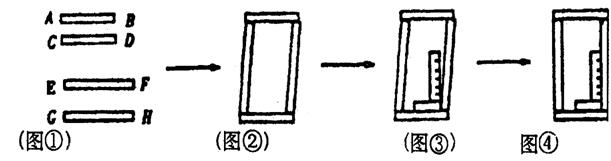
22.工人师傅做铝合金窗框分下面三个步骤进行：(6分)
先找出两对符合规格的铝合金窗料(如图①)，使AB=CD，EF=GH；然后做成如图②的四边形，则这时窗框的形状是_________形，根据的数学道理是：_________________________________________________.
(3)将直角尺靠紧窗框的一个角(如图③)，调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时(如图④)，说明窗框合格，这时窗框是_________形，根据的数学道理是：_______________________.
三、解答题：（总分51分）
23、计算：（每小题4分，计8分）
（1）、
（2）、
（3）、
—
24、画图题：（4分）
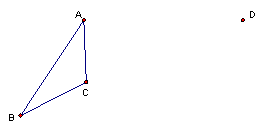
把△ABC的顶点A平移到点D处，请你作出平移后的△DEF。
25、如图，在四边形ABCD中，AC⊥DC，△ADC的面积是30cm2，DC = 12cm AB = 3cm BC=4cm ，求△ABC得面积是多（6分）
 |
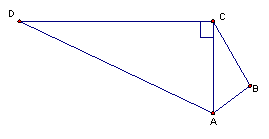26、已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF。
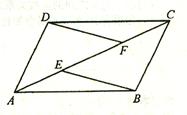求证：（1）△ADF≌△CBE；（2）EB∥DF。（10分）
27、如图，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连结C′E．（11分）
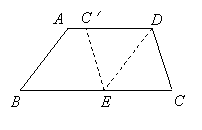（1）求证：四边形CDC′E是菱形．
（2）若BC=CD+AD，试判断四边形ABEC的
形状，并加以证明。
28、如图，矩形ABCD中，M是AD的中点。（12分）
（1）、求证：△AB≌△DCM；
（2）请你探索，当矩形ABCD的一组邻边满足何种数量关系时，有BM⊥CM成立，说明你的理由。
 |
A M D
B C