§16.1---平行四边形的性质综合练习
广东实验中学附属天河学校数学教师 张友兵
一、 教学目标：
1、通过适量的练习，促使学生进一步加深对平行四边形的性质的理解与运用。（平行四边形的性质从对边的关系，四个内角的关系，对角线的关系逐一梳理。）
2、培养学生在应用中，从诸多的知识点识别选用，有理有据的思辩能力。
3、激发学生的学习热情，促进学生的更高说理能力。
二、 教学重点：
1、对平行四边形的性质的应用。
2、与平行四边形的性质相关联的拓展思考。
三、 教学难点：
1、对知识点的题设与结论加图形的综合思考。
2、形数结合，用数学方法的能力的培养。
四、 教学准备：
学案一份、实物投影仪、彩色粉笔，多媒体（选用）
五、 复习练习过程：
（1）回顾思考，完成表格：
| 边的关系 | 角的关系 | 对角线的关系 | 图形的对称性 | |
| 平行四边形 |
（2）从平行四边形的一个钝角顶点引分两边的垂线，如果这两条垂线间的夹角为75
，求这个平行四边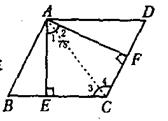
形各内角的度数。
（这是一题一般四边形与平行四边形的结合问题。注意提示学生画
图，分解问题，从最紧要的联系点开始。）
答案：∠BAD= ∠C=1800-750=1050,∠B=∠D=1800-1050=750
(3) 在▱ABCD中，∠A的平分线分BC 成4㎝与3㎝的两条线段，求▱ABCD的周长。
(4) 如图，在▱ABCD中，已知AC、BD相交于点O，两条对角线的和为24cm,BC长为8cm，
求△AOD的周长。
 |
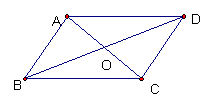(5) 如图，在▱ABCD中，过点P画线段EF、GH分别平行于AB、BC，试找出图中的平行四边形，
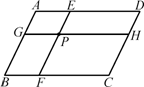与你的同伴比一比，看看谁找出的多．
(对平行四边形的定义的直接应用。)
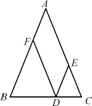(6) 如图，D是等腰三角形ABC的底边BC上的一点，E、F分别在AC、AB上，且DE∥AB， DF∥AC．试问DE、DF与AB之间有什么关系吗?请说明理由．
(7) 如下图，AD∥CD，AC、BD相交于点O，则面积相等的三角形有＿＿＿对
 |
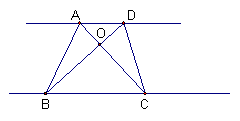（8）已知三条线段的长分别是22㎝，16㎝和18㎝，以哪两条为对角线，其余一条为边，可以画出
平行四边形？进而讨论，如果以a、b为对角线，以c为一边画平行四边形的话，a、b、c间应
满足什么关系？（设a>b）
(9) 如图，在△ABC中，BD平分∠ABC，DE∥BC交AB于点E，EF∥AC交BC于点F，
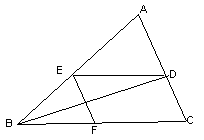试说明：BE=CF
六、 你的学习收获：