1:把同类项的系数相加，所得的结果作为系数，字母和字母的指数保持不变
2: “
都为正整数）”和语言表述“同底数幂相乘，底数不变，指数相加，幂的乘方，底数不变，指数相乘，积的乘方，等于把积的每一个因式分别乘方”
本节的难点是： （1）正确运用有关的运算法则，防止发生以下的运算错误，如：
等； （2）正确处理运算中的“符号”，避免以下错误，如：
等； （3）在进行加、减、乘、除、乘方的混合运算时处理好运算程序问题，防止用运算程序混乱产生的错误，如
……等等．
典型例题
例1 计算： 
例2 
【点评】
当两个幂的底数互为倒数或负倒数时，底数的积为1或－1．这时逆用积的乘方公式可起到简化运算的作用．
例3 
例4
求下列各式中的
：【
【点评】
由幂的意义，我们容易知道，两个幂相等时，如果底数相同，则指数一定相同；但如果指数相同，其底数应就指数为奇数和偶数两种情况进行研究．当指数为奇数时，则底数相同；当指数为偶数时，则底数相同或互为相反数．
例5 
【分析】
（1）比较两个数的大小．常用比较法即考察两数差的值．当差为正数时，第一量大于第二量；当差为零时，第一量等于第二量；当差为负数时，第一量小于第二量．即
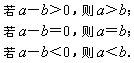
技能训练
（一）选择题
……………………………………………………………………（ ）
………………………………………………（ ）
……………………………………………………………………（ ）
…………………………………………………………………（ ）
（二）填空题：
【 
（三）计算题：
【 
整式的练习
1：【同步达纲练习】、填表
3.1 整式
1.填空：
(1)下列代数式中，单项式是 个，多项式有 个。
-2x2y、
、-
、a、
、
、-
x2+2x-1
(2)单项式-
的系数是
，次数是
.
(3)多项式3a-4a2b+
的项分别为
，最高次项的次数为
，常数项为
。
(4)多项式x6-y6是 次 项式
(5)多项式ab4c-5ax+7是 次 项式，其中最高次项的系数是 ，常 数项是 。
(6)关于x的多项式(a-4)x4-xb+x-b为二次三项式，那么a ，b ；若x=-3 ，那么二次三项式的值为 。
(7)若(4a-4)x2yb+1是关于x、y的七次单项式，则方程ax-b=x-1的解为 。
(8)若-
为整数，则整数m为 。
2.选择
(4)多项式32πx5-4x是( )
A.五次二项式 B.六次二项式
C.七次二项式 D.八次二项式
(5)把多项式x2y+y3-
xy2-3x3按x的升幂排列为( )
A.y3-3x3+x2y- xy2
B.-xy2-3x3+y3+x2y
C.-3x3+x2y- xy2+y3 D.y3- xy2+x2y-3x3
3.把下列各代数式填在相应的括号里
x-7 x
4ab 
5-
y 
x+
x２+
+1
-1
单项式集合：｛ …｝
多项式集合：｛ …｝
整式集合：｛ …｝
4.将多项式2xy2-x2y-x3y3-7按x降排列再按y升排列
5.已知多项式-
x2ym+1+xy3-3x3+6是五次四项式，而单项式7x 3ny5-mz的次数与该多项式的次数相同，求n的值。
3.2 整式的加减
【双基同步训练】
1.填空
(1)在多项式3x2y-xy2-x2y+5xy2-4中，3x2y与 是同类项
，-xy2与 是同类项。
(12)已知A=3x2-2x+1，B=2x2+x-3，C=-5x2-3x+4，那么A-B+C= ，-A+B-C= 。 (14)(-7a2b)-(+2a2b)+(-3a2b)=
(16)7x2-［-2x2+(-6x+8x2+4)］=
2.选择
(1)下列各式正确的是( )
A.3x2-3x2=x2 B.m2+m3=m5
C.4x2-2x2=2 D.5a4b3-4b3a4=a4b3
(6)已知256b和5ma2mb是同类项，则m的值为( )。
A.2 B.3 C.6 D.2或3
(7)已知：4x5y2和-3x3my2是同类项，则代数式12m-24的值为( )。
A.-3 B.-5 C.-4 D.-6
(10)下列各组中的两个单项式，属于同类项的是( )。
A.6xy和6xyz B.-125和-a3
C.7a2b和-ab2
D.0.73xy4和-2y4x
(11)合并多项式7a2b-51a2b的同类项的结果是( )。
A.-44a2b B.-44C.-44a4b2 D.44a2b
(12)下列各组中的两个单项式，不是同类项的是( )。
A.-54xy和3yx B.a2b2和-a2b2
C.3.5a2b和a2c D.-64和43
4.合并同类项
(1)(6m2-4mn-3n2)-(2m2-4mn+n2)
(2)-(-2x2+3x3-4)+(-7x+5x2+2x3)
(3)2a-3a+5a-7a
(4)
(5)5a2b-3ab2-7a2b+ab2
(6)7m-3n+5m+3n
(8)-17(3x+5y)+21(3x+5y)+4(3x+5y)
参考答案
3.1 整式
【双基同步训练】
1.(1)—(4)略 (5)略 (6)a=4，b=2，-14 (7)x=
(8)m=0、-1 (9)m+n =0，m2-n2=0，│2m│-2│n│=0 (10)│x-y│=5
(11)-8
2—5. 略
6.略
7.b＜-a＜a＜-b
【创新能力训练】
略
【实践能力训练】
略
3.2 整式的加减
【双基同步训练】
1.(1)—(6)略 (7)2x-3y+1 (8)-3a-5b+6 (9)y2-4y+4 (10)7z-1 (11)(am-bm)-(an-b n) (12)-4x-6x+8，4x2+6x-8 (13)11x2 (14)-12a2b (15)2xn (16)x2+6x-4 (17)-9a2b-2ab2+4ab (18)9xy-7 (19)-6m2+8m+11 (20)2m2-mn-n2
2.(1)—(5)略 (6)B (7)C (8)B (9)D (10)D (11)A (12)C (13)D (14)C (15)D (16)A
3.略
4.(1)—(2)略 (3)-3a (4)-
x (5)-2a2b-2ab2 (6)12m (7)①-7(2 a-b)2；②8(3x+5y)
5.(1)略 (2)
x+
(3)0 (4)-69 (5)2.96 (6)-8
(7)8 (8)8，32 (9)-16
6.(1)20x3 (2)x2-xy-4y2 (3)16a+3b (4)4xy-
y2
7.(1)2x2-4x-5 (2)14x2-23x+10
8.(1)x2-8xy+y2 (2)2x2-8xy