《勾股定理》复习题B
一、填空题（每题3分，共24分）
1．三角形的三边长分别为 a2＋b2、2ab、a2－b2（a、b都是正整数），则这个三角形是（ ）
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
2．若△ABC的三边a、b、c满足a2＋b2＋c2十338＝10a＋24b＋26c，则△ABC的面积是（ ）
A.338 B.24 C.26 D.30
3．若等腰△ABC的腰长AB＝2，顶角∠BAC＝120°，以 BC为边的正方形面积为（ ）
A.3 B.12 C.
D.
4．△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（ ）
A.42 B.32 C.42 或32 D.37 或 33
5．直角三角形三条边的比是3∶4∶5.则这个三角形三条边上的高的比是（ ）
A.15∶12∶8 B. 15∶20∶12 C. 12∶15∶20 D.20∶15∶12
6．在△ABC中，∠C＝90°，BC＝3，AC＝4.以斜边AB为直径作半圆，则这个半圆的面积等于（ ）
A.
B.
C.
D.25π
7．如图1，有一块直角三角形纸片，两直角边AC＝6cm，BC＝8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）
A.2cm B.3 cm C.4 cm D.5 cm
 | |||
 | |||
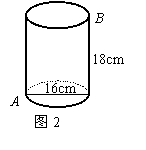
8．如图2，一个圆桶儿，底面直径为16cm，高为18cm，则一只小虫底部点A爬到上底B处，则小虫所爬的最短路径长是（π取3）（ ）
A.20cm B.30cm C.40cm D.50cm
二、填空题（每小题3分，共24分）
9．在△ABC中，若其三条边的长度分别为9、12、15，则以两个这样的三角形所拼成的长方形的面积是＿＿＿．
10．一个长方体同一顶点的三条棱长分别是3、4、12，则这个长方体内能容下的最长的木棒为＿＿＿.
11．在△ABC中，∠C＝90°，BC＝60cm，CA＝80cm，一只蜗牛从C点出发，以每分20cm的速度沿CA→AB→BC的路径再回到C点，需要＿＿＿分的时间．
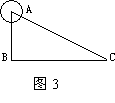
12．如图3，一艘船由岛A正南30海里的B处向东以每小时20海里的速度航行2小时后到达C处.则AC间的距离是＿＿＿．
13．在△ABC中，∠B＝90°，两直角边AB＝7，BC＝24，三角形内有一点P到各边的距离相等，则这个距离是＿＿＿．
14．已知两条线段长分别为5cm、12cm，当第三条线段长为＿＿＿时，这三条线段可以组成一个直角三角形，其面积是＿＿＿．
15．观察下列一组数：
列举：3、4、5，猜想：32＝4+5；
列举：5、12、13，猜想：52＝12+13；
列举：7、24、25，猜想：72＝24+25；
…… ……
列举：13、b、c，猜想：132＝b+c；
请你分析上述数据的规律，结合相关知识求得b＝＿＿＿，c＝＿＿＿.
16．已知：正方形的边长为1.（1）如图4（a），可以计算出正方形的对角线长为
；如图（b），两个并排成的矩形的对角线的长为＿＿＿；n个并排成的矩形的对角线的长为＿＿＿.（2）若把（c）（d）两图拼成如图5“L”形，过C作直线交DE于A，交DF于B.若DB＝
，则 DA的长度为＿＿＿．
 |
三、解答题（共58分）
17．如图6，折叠长方形一边AD，点D落在BC边的点F处，BC＝10cm，AB＝8cm，求：(1)FC的长；(2)EF的长．
18．为了丰富少年儿童的业余生活，某社区要在如图7所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB＝25km，CA＝15km，DB＝10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等?
19．一艘渔船正以30海里／时的速度由西向东追赶渔群，在A处看见小岛C在船北偏东 60°.40分钟后，渔船行至 B处，此时看见小岛 C在船的北偏东30°，已知小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续航行（追赶鱼群），是否有进入危险区的可能？
20．在Rt△ABC中，AC＝BC，∠C＝90°，P、Q在AB上，且∠PCQ＝45°试猜想分别以线段AP、BQ、PQ为边能组成一个三角形吗？若能试判断这个三角形的形状．
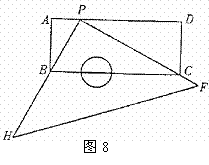21．如图8，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合)，在AD上适当移动三角板顶点P：
①能否使你的三角板两直角边分别通过点B与点C？若能，请你求出这时 AP 的长；若不能，请说明理由．
②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH 始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，能否使CE＝2cm？若能，请你求出这时AP的长；若不能，请你说明理由．
参考答案
一、1．A 2．D 3．B 4．C 5．D.提示：由三角形面积公式，可得
·AB·CD＝·BC·AC.设BC＝3k，AC＝4k，AB＝5k，则5k·CD＝2k·4k.所以CD＝
k.所以AC∶BC∶CD＝4k∶3k∶
k＝20∶15∶12；6．A.提示：在Rt△ABC中，由勾股定理可以得到AB2＝42+32＝25，所以AB＝5.所以半圆的面积S＝π
＝
π；7．B 8．B.
二、9．108 10．13 11．12 12．由勾股定理，可以得到AB2+BC2＝AC2，因为AB＝30，BC＝20×2＝40，所以302+202＝AC2，所以AC＝50，即AC间的距离为50海里；13．3 14．13cm或
cm，30cm2或
cm2 15．84、85 16．
、
、.
三、17．(1)在Rt△ABC中，由勾股定理可以得到AF2＝AB2+BF2，也就是 102＝82+BF2.所以BF＝6，FC＝4(cm) (2)在Rt△ABC中，由勾股定理，可以得到EF2＝FC2+(8－EF)2.也就是EF2＝42+(8－EF)2.所以EF＝5(cm)
18．10米；
19．设小岛C与AB的垂直距离为a，则易求得a2＝300＞102，所以这艘渔船继续航行不会进入危险区；
20．能组成一个三角形，且是一个以PQ为斜边的直角三角形.理由是：可将△CBQ绕点C顺时针旋转90°，则CB与CA重合，Q点变换到Q′点，此时，AQ′＝BQ，△APQ′是直角三角形，即AP2＋AQ′2＝PQ′2，另一方面，可证得△CPQ′≌△CPQ（SAS），于是，PQ′＝PQ，则AP2＋BQ2＝PQ2.
21．①能.设AP＝x米，由于BP2＝16+x2，CP2＝16+(10－x)2，而在Rt△PBC中，有BP2+ CP2＝BC2，即16+x2+16+(10－x)2＝100，所以x2－10x+16＝0，即(x－5)2＝9，所以x－5＝±3，所以x＝8，x＝2，即AP＝8或2，②能.仿照①可求得AP＝4.