八年级数学下册第十六章《分式》整章水平测试（A）
山东 赵卫东
一、 试试你的身手（每小题3分，共30分）
1．若
有意义，则
的取值范围是
．
2．若分式
的值为零，则的值为
．
3．不改变分式的值，把分式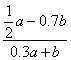
的分子与分母的各项系数化为整数为： ．
4．当
时，分式
的值不小于0．
5．化简：
=
．
6． 若
，则
的值是
．
7．计算
=
．
8．生物学家发现一种病毒的长度约为0.000043㎜，用科学记数法表示0.000043的结果为 ㎜．
9．若方程
有增根，则的值可能是
．
10．把题目补充完整：轮船在顺流中航行64km与逆流中航行34km一共用去的时间等于该船在静水中航行180km所用的时间，已知水流的速度是每小时3km，求该船 ．
设
，依题意列方程
．
二、相信你的选择（每小题3分，共30分）
1．在有理式
中，分式有（ ）．
（A）1个 （B）2个 （C）3个 （D）4个
2．x为实数，下列式子一定有意义的是（ ）．
（A）
（B）
（C）
（D）
3．如果
=0，则等于（ ）．
（A）±2 （B）－2 （C）2 （D）3
4．分式
中的
同时扩大2倍，则分式的值（ ）．
（A）不变 （B）是原来的2倍 （C）是原来的4倍 （D）是原来的
5．下列各式从左到右的变形正确的是（ ）．
（A）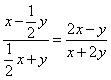
（B）
（C）
（D）
6．已知
，
，则M与N的大小关系为（ ）．
（A）M>N （B）M=N （C）M<N （D）不确定
7．已知
，则
的值为（ ）．
（A）
（B）
（C）
（D）―
8．关于的方程
的解是负数，则的取值范围是（ ）．
（A）=3 （B）<3且≠－1 （C）≥3
（D）≤3且≠－1
9．在正数范围内定义一种运算“※”，其规则为※
=
，根据这个规则方程※（
）=0的解为（ ）．
（A）1
（B）0
（C）无解
（D）
10．学生有
个，若每
个人分配1间宿舍，则还有一人没有地方住，问宿舍的间数为（ ）．
（A）
（B）
（C）
（D）
三、挑战你的技能（本大题共48分）
1．（本题8分）化简：
2．（本题8分）解方程：
3．（本题10分）先化简代数式
，然后请选择一组你喜欢的
的值代入求值．
4．（本题11分）小明在计算
，
，
，…时发现
，
，
，…
（1）用式子表示这一变化规律；
（2）利用这一规律计算：
5．（本题11分）同一条高速公路沿途有三座城市A、B、C，C市在A市与B市之间，A、C两市的距离为540千米，B、C两市的距离为600千米．现有甲、乙两辆汽车同时分别从A、B两市出发驶向C市，已知甲车比乙车的速度慢10千米/时，结果两辆车同时到达C市．求两车的速度．
四、拓广探索（本大题共12分）
请阅读某同学解下面分式方程的具体过程．
解方程
解：
，
①
，
②
，
③
∴
④
∴
把
代入原方程检验知是原方程的解．
请你回答：
（1）得到①式的做法是
；得到②式的具体做法是
；得到③式的具体做法是
；得到④式的根据是
．
（2）上述解答正确吗？如果不正确，从哪一步开始出现错误？答：
．错误的原因是
．
（3）给出正确答案（不要求重新解答，只需把你认为应改正的加上即可）．
参考答案：
一、1．
且
2．1 3．
4．≤
5．
6．
7．
8．
9．6 10．在静水中的速度，船在静水中的速度为km/h，
．
二、1．D 2．A 3．C 4．B 5．A 6．B 7．B 8．B 9．D 10．C
三、1．
2．无解．
3．
，答案不唯一．
4．（1）
；（2）
5．甲车的速度为90千米/ 时，乙车的速度为100千米/ 时．提示：设乙车的速度为千米/ 时，则甲车的速度为（
）千米/ 时，由题意可得方程：
四、（1）移项，方程两边分别通分，方程两边同除以
，分式值相等，分子相等，则分母相等；
（2）有错误．从第③步出现错误，原因：可能为零；
（3）当
时，
，
经检验知
也是原方程的解，
故原方程的解为