
 《不等式》复习达标检测
《不等式》复习达标检测
一、选择题(每小题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1.由x<y得到ax>ay,则a的取值范围是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
2.不等式![]() x<2的非负整数解有( )
x<2的非负整数解有( )
A.4个 B.5个 C.3个 D.2个
3.-5x>3的解集是( )
A.x>-![]() B.x≥-
B.x≥-![]() C.x<-
C.x<-![]() D.x≤-
D.x≤-![]()
4.不等式组![]() 的解集是(
)
的解集是(
)
A.![]() ≤x≤4 B.
≤x≤4 B.![]() <x≤4 C.
<x≤4 C.![]() <x<4 D.
<x<4 D.![]() ≤x<4
≤x<4
5.在数轴上表示不等式x≥-2的解集,正确的是( )
A.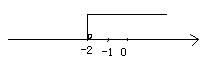 B。
B。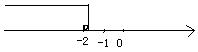
C.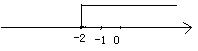 D。
D。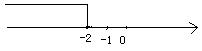
6.满足不等式组![]() 的整数m的值有( )
的整数m的值有( )
A.1个 B.2个 C.3个 D.4个
7.若方程组![]() 的解x,y满足0<x+y<1,则k的取值范围是( )
的解x,y满足0<x+y<1,则k的取值范围是( )
A.-4<k<0 B.-1<k<0 C.0<k<8 D.k>-4
8.某种植物适宜生长温度为18~20的山区,已知山区海拔每升高100米,气温下降0.55,现测得山脚下的气温为22,问该植物种在山上的哪一部分为宜?如果设该植物种植在海拔高度为x米的山区较适宜,则由题意可列出的不等式组为( )
A.18≤22-![]() ×0.55≤20
B.18≤22-
×0.55≤20
B.18≤22-![]() ≤20
≤20
C.18≤22-0.55x≤20
D.18≤22-![]() ≤20
≤20
10.已知关于x的不等式组![]() 的解集为3≤x<5,则
的解集为3≤x<5,则![]() 的值为(
)
的值为(
)
A.-2
B.- ![]() C.-4 D.-
C.-4 D.-![]()
二.填空题(每小题4分,共40分)
11.若![]() x2m-1-8>5是关于x的一元一次不等式,则m=__ ___。
x2m-1-8>5是关于x的一元一次不等式,则m=__ ___。
12.若x<-1,则x___ __![]() (填“>”、“<”)。
(填“>”、“<”)。
13.不等式6-12x<0的解集是___ __。
14.如果一次函数y =(2-m)x+m的图象经过第一、二、四象限,那么m的取值范围是________________________。
15.不等式组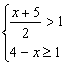 的非负整数解是__ ___。
的非负整数解是__ ___。
16.若不等式(2k+1)x<2k+1的解集是x>1,则k的范围是__ ___。
17.如果不等式3x-m≤0的正整数解是1,2,3,那么k的范围是___ __。
18.如果n是一个正整数,且它的3倍加10不小于它的5倍减2,则n为__ ___。
19.已知关于x的方程组![]() 的解满足x>y,则p的取值范围是_ ____。
的解满足x>y,则p的取值范围是_ ____。
20.一位老师说,他班学生的一半在学数学,四分子一的学生在学音乐,七分之一的学生在学外语,还剩不足6名同学在操场上踢足球,则这个班的学生共有__ ___人。
三.解答题(共70分)
21.(10分)解下列不等式,并把它的解集在数轴上表示出来。
(1)2(x+1)-3(x+2)<0
(2)![]() <
<![]() -2
-2
22.(10分)解下列不等式组:
(1)![]() (2)
(2)![]()
23.(10分)当m为何值时,方程组![]() 的解是正数?
的解是正数?
24.(10分)当m取何值时,关于x的方程3x+m-2(m+2)=3m+x的解在-5和5之间?
25、(10分)某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品,共50件。已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你给设计出来。
(2)设生产A、B两种产品获总利润为y(元),其中一种的生产件数为x,试写出y与x之间的函数关系式,并利用函数的性质说明(1)中哪种生产方案获总利润最大?最大利润是多少?
26、(10分)我校组织学生去参加数学夏令营,住在云龙饭店.若每个房间住4人,则剩下3人没处住;若每个房间住8人,则空一房间,并且还有一房间既不空也不满.那么可能有多少间房和多少名学生?
27.(10分)某自行车保管站在某个星期日接受保管的自行车共有3500辆,其中变速车保管费时每辆一次0.5元,一般车保管费是每辆0.3元。
(1)若设一般车停放的辆数为x,总保管费的收入为y元,试写出y与x的关系式;
(2)若估计前来停放的3500辆自行车,变速车的辆数不少于25%,但不大于40%,试求该保管站这个星期日保管费收入总数的范围。