八年级数学上学期水平自测题（A）
一、填一填（每空3分，共30分）
1． 若a>b， a+2 b+2；-a -b （填“<”或“>”）
2．若a+b＞2b+1,则a----------b。
3.在数0，-4，4，-4
，-6.2，-2，-16中， 是方程x+4=0的解；
能使不等式x+4>0成立； 能使不等式x+4<0成立。
4．用代数式表示，比x的5倍大1的数不小于x的
与4的差
。
5． 比较大小
（填“<”或“>”）
6．已知a，b是常数(a≠0)，不等式ax+b>0。当 时，不等式的解集是x>-
；当 时，不等式的解集是x<-。
二、选一选：（每题3分，共30分）
7．在下列表达式中，是不等式的有（ ）
① -2＜0 ②2x+3y<0 ③ x=-1 ④x2+3x-1 ⑤ x+2y=4 ⑥ x+3<y-3
A、1个 B、2个 C、3个 D、4个
8．在数轴上表示不等式
≥－2的解集，正确的是（ ）
A B C D
9．下列式子中，不成立的是
A、－2>－l B、3>2 C、O>－l D、2>－1
10．无论x取什么数,下列不等式总成立的是( ).
A、x+5＞0； B、x+5＜0； C、(x+5)2＜0； D、(x-5)2≥0
11．下列叙述不正确的是( )
A、若x<0，则x2>x B、如果a<-1，则a>-a
C、若
，则a>0 D、如果b>a>0，则
12．如果(m-1)x<m-1 的解集是x>1,那么m满足（ ）
A、m〈-1 B、m〉-1 C、m〈1 D、m〈-1
三、想一想（每题10分共40分）
13. 根据不等式的性质，把下列不等式化为x＞a或x＜a的形式（a为常数）
(1)
(2)
(3)-3x+5>-7 (4)2x–5>0
2.小亮家距离学校的路程是5km，某天骑车去上学，上午7：40从家出发，先以16千米/时的速度行驶了x小时，后又加快了速度以20千米/时的速度行驶，结果在8：00之前赶到了学校，请你列出不等式
3.按照下列条件，写出仍能成立的不等式，并注明理由．
(1)若a＜b两边都加-5；(2)若-2a＜b两边都除以-2；
(3)若3a≤-b两边都除以3；(4)若a≤b两边都加上c；
(5)若a＜b两边都乘上c．
4．用计算器探究：
比较下列算式的结果的大小（1） 
（2）
（3）
（4）
根据上述各题运算结果猜想 ：
（a>b>0，a，b是整数）并再举几个实例。
答案及提示：1.>
< 2. > 3.
–4；0、4、-2； -4、-6.2、-16 4.5x+1≥
5. > 6. a>0 a<0 7.C 8.C
9.A 10.D 11.B
12.C 13.(1)x>3 (2)x>8 (3) x<4 (4)x>
14. x+
15.
解：(1)a-5＜b-5，(不等式基本性质1)
(5)因为不等式两边乘以c，而c是字母代替数，因此c有三种情况，① c＞0，②c＜0，③c=0
当c＞0时，ac＜bc(基本性质2)
当c＜0时，ac＞bc(基本性质3)
当c=0时，ac = bc
16.>
< < < 0<b<a≤3 时， > ；a>3时
<
13．1～13.2水平自测题（B）
一、填一填（每空3分，共30分）
1.用不等式表示：的3倍与1的差不大于2与的和的一半，得_____。
2.若a<b<0，则a2 ab
3.x适合-1≤x＜2，且x是整数，则x的值是 。
4．有一个两位数，个位上的数是a，十位上的数是b，如果把这个两位数的个数和十位对调，得到的两位数小于原来的两位数，那么a b
5.写出满足x+2 >-3 的负整数x的值是 。
6．某种出租车的收费标准是：起步价7元（即行驶距离不超过3千米都需要付7元车费），超过3千米，每增加1千米，加收2.4元（不足1千米按1千米计），某人乘这种出租车从甲地到乙地共支付车费19元，设此人从甲地到乙地经过的路程是x千米，那么x的最大值是
二、 选一选 （每题3分，共30分）
7．设“○”、“□”、“△”分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个“○”、“□”、“△”这样的物体，按质量从大到小的顺序排列为（ ）
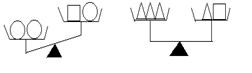A、 ○□△
B、 ○△□
C 、 □○△ D、 △□○
8．如果t>0,那么a+t与a的大小关系是 ( ).
A、a+t>a B、a+t<a C、a+t≥a D、不能确定
9．如果a<b，那么下列不等式（1）a-4<b-4；(2)a-b>0；(3)a-a<b-a；(4)a+5>b-5中，正确的个数有（ ）个
A、 1 B、 2 C、 3 D、 4
10．若
<1，则 （
）
A、x>1 B、x<1 C、x<0 D、x<0或 x>1
11．设
的大小是（ ）
A、 
； B 、
；
C 、
； D 、
12．天平右盘中的每个砝码的质量都是1g，则物体A
的质量m(g)的取值范围，在数轴上可表示为
 | |||
 |
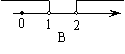
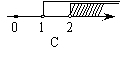三、想一想
13．根据不等式的性质，把下列不等式化为x＞a或x＜a的形式（a为常数）
（1） 5x< 3x-2 (2) 
< 4-x (3)4x
>-x+3 (4)
14．梦昊同学准备用压岁钱180元钱请同学去听科普讲座，门票每张15元。若把好朋友都请上他最少要买x张票。倘若留出往返车费至少16元，请列出不等式。
15.（1）比较下列算式的结果的大小：
2×3×4； 
2×（-1）×2
2×4×4。
（2）观察以上各式反映的规律，并用一个含有字母a、b的式子表示出来 。
（3）请用我们学过的知识说明它的正确性。
16．已知：两个正整数的和与积相等，求这两个正整数．
解：不妨设这两个正整数为a、b，且a≤b．
由题意，得ab=a+b，…………………………(*)
则ab=a+b≤b+b=2b，所以a≤2．
因为a为正整数，所以a=1或2．
①当a=1时，代入等式(*)，得1·b=1+b，b不存在；
②当a=2时，代入等式(*)，得2·b=2+b，b=2．
所以这两个正整数为2和2．
仔细阅读以上材料，根据阅读材料的启示，思考是否存在三个正整数，它们的和与积相等?试说明你的理由．
答案及提示：1.
3x-1≤
2. > 3.
–1,0,1 4. < 5. –1、-2、-3、-4 6. 8
7. A 8. A 9. B 10. D 11. C 12.A
13．（1）x<-1 (2)x>-6 (3)x>
(4)x<
14. 180-15x≥16 15. (1)> > = (2) a2+b2≥2ab (3) 因为（a-b）2 ≥0,故 a2+b2≥2ab
16．解：假设存在三个正整数，它们的和与积相等．
不妨设这三个正整数为a、b、c，且a≤b≤c，则abc=a+b+c (※)
所以abc=a+b+c≤c+c+c=3c，所以ab≤3，
若a≥2，则b≥a≥2，所以ab≥4，与ab≤3矛盾。
因此a=l，b=l或2或3，
① 当a=l，b=l时，代入等式(※)得l+l+c=1·1·c，c不存在；
⑦ 当a=l，b=2时，代入等式(※)得1+2+c=1·2·c，c=3；
③ 当a=1，b=3时，代入等式(※)得1+3+c=1·3·c，c=2；与b≤c矛盾，舍去
所以a=1，b=2，c=3，因此假设成立．即存在三个正整数，它们的和与积相等．