第十三章 全等三角形
一、概念：
全等形：能够完全重合的图形叫做全等形.
全等三角形：能够完全重合的两个三角形叫做全等三角形.
对应顶点、对应边、对应角：把两个全等的三角形重合到一起.重合的顶点叫做对应顶点；重合的边叫做对应边；重合的角叫做对应角.
二、全等三角形的性质：全等三角形的对应边相等、对应角相等.
三、三角形全等的条件：
1. 三边对应相等的两个三角形全等（可以简写成“边边边”或“SSS”）.
2. 两边和它们的夹角对应相等的两个三角形全等（可以简写成“边角边”或“SAS”）.
3. 两角和它们的夹边对应相等的两个三角形全等（可以简写成“角边角”或“ASA”）.
4. 两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）.
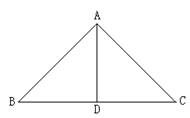例1.在△ABC中，AB=AC，AD是三角形的中线.
求证：△ABD≌△ACD
例2.如图所示，直线AD、BE相交于点C，AC=DC，BC=EC.
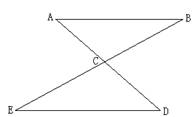求证：AB=DE
例3.如图所示，D在AB上，E在AC上，AB=AC, ∠B=∠C.
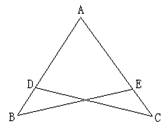求证：AD=AE
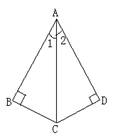例4.如图，AB⊥BC, AD⊥DC, ∠1=∠2.
求证：AB=AD
练习：
1. 如图（1），如果△AOC ≌ △BOD，则对应边是__________，对应角是_____________；
如图（2），△ABC
≌ △CDA，则对应边是_____________，对应角是_______________；
2. 已知
≌
，A与
，
与
是对应顶点，的周长为10cm，AB =3cm，BC =4cm. 则
=
cm，
=
cm，
=
cm.
3. 已知≌
，A与D，B与E分别是对应顶点，
， 
，BC
=15cm，则
=
，FE = cm.
4. 已知，如图，△AEC ≌ △ADB,△BEC ≌ △CDB.你能写出它们的对应边和对应角吗？
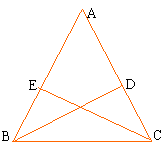
5. 如图，点E, F在BC上，BE=CF, AB=DC, ∠B=∠C.
求证: ∠A=∠D
 |
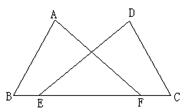6. 如图，△ABC
≌ 
，
和
是对应角，AB
= AD是对应边，写出另外两组对应边和对应角.
|
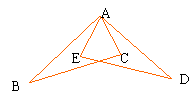
7. 如图，△ABC ≌
△A′B′C′，∠C =25°,BC =6cm, AC
=4cm, 你能得出△A′B′C′中哪些角的大小、哪些边的长度？
8. 如图，△ABD ≌ △EBD, △DBE ≌ △DCE, B, E, C在一条直线上.
（1） BD是∠ABE的平分线吗？为什么？
（2） 
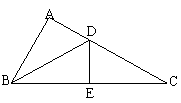DE⊥BC吗？为什么？
（3） 点E 平分线段BC吗？为什么？
9. 将一几何图形放在平面镜前，则该图形与镜子里的图形全等，因为它们的______________相同
10. 如图，AB =CD，AD =BC，O为BD上任意一点，过O点的直线分别交AD，BC于M、N点.
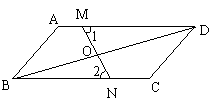求证：
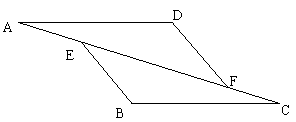
11. 如图在
和
中，点A，E，F，C在同一条直线上有下面四个论断：
（1）AD
=CB ， （2）AE =CF ， （3）
， （4）AD
//BC .
请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程.
12. 填空题：
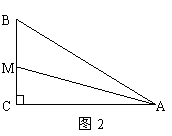
(1)如图1，已知:AC
=DB，要使≌
，只需增加一个条件是_____ ____.
(2)如图2,已知:中，
，AM平分
，CM
=20cm那么M到AB的距离
是 .
(3)如图3,已知:在和中，如果AB
=DE，BC =EF，只要找出
=
或 =
或 // ，就可证得≌.
（4）. 已知:如图4，AB =EB，∠1=∠2，∠ADE =120°，AE、BD相交于F，则∠3的度数为___ ___．
（5）. 如图5, 已知：∠1 =∠2 , ∠3 =∠4 , 要证BD =CD , 需先证△AEB ≌△A EC , 根据是_________再证△BDE ≌△__ ____ , 根据是__ ________．
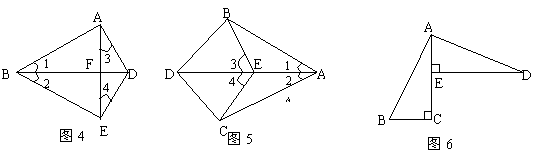（6）.
已知：如图6 , AC
BC于C , DEAC于E , ADAB于A , BC =AE．若AB = 5 , 则AD =___________．