第17章 创 新 能 力 测 试 题
（时间：120分钟 满分120分）
一、填空题（每小题3分，共30分）
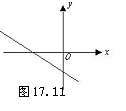1．一次函数y=ax+b图象如图所示，则其
a、b的符号为_______．
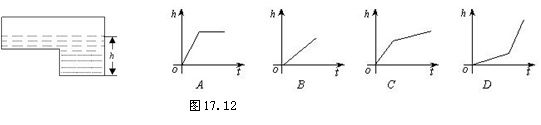
2．如图是某蓄水池的横断面示意图，
分为深水池和浅水池，如果这个蓄水池以固定的流量注水，
下面能大致表示水的最大深度h与时间t之间的关系的图象是 ．
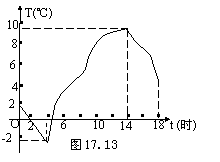3．图17.13所示的是某城市冬季某一天的气温随
时间变化图，这一天的温差为____℃；
当t________范围内，气温逐渐升高．
4．以点p(0,－1)为圆心,3为半径画圆,分别交y轴
的正半轴、负半轴于点A、B，则A点坐标为
______，B点坐标为_______．
5．如果水的流速是a米/分(a为定量),那么每分钟的进水量Q(立方米)与所选择的水管直径D(米)之间的函数关系是 ,其中自变量是 ,常量是 ．
6．已知点M（3，－2）与点N（x，y）在同一条平行于y轴的直线上，且N到x轴的距离等于4，那么点N的坐标是 ．
| |
第二象限上的一点，PD⊥
轴于点D，则△POD的面积为___________．
8．点P(2a－1,3+a)，若p点在x轴的上方、y轴的左侧，则a的取值范围是____．
9．当x≥3时，函数y=2x+5的最小值为____．
10．已知一次函数y1=–2x–3和y2=x，当x_________时，y1>y2．
二、选择题（每小题3分，共24分）
11．平面直角坐标系中，点A（2，3）关于x轴对称的点的坐标是（ ）
A．（2，﹣3） B．（﹣2，3） C（﹣2，﹣3） D．（3，2）
12．已知正比例函数y=(3k—1)x，若y随x的增大而增大，则k的取值范围是（ ）
A ．k＜0 B．k＞ 0 C．k ＜
D．k＞
13．某人骑车外出，所行的路程S(km)与
时间t(h)的函数关系如图17.14所示，现有下列四种
说法：①第3小时中的速度比第1小时中的速度快；②第3小时中的速度比第1小时中的速度慢；③第3小时后已停止前进；④第3小时后保持匀速前进．其中说法正确的是（ ）
A．②、③ B．①、③ C．①、④ D．②、④
14．已知函数y=–
的图象过点（－2，3），那么下列各点在函数y=kx－2的图象上的是 （ ）
A．（4，1） B．（
，－1） C．（－
，－11） D．（－3，－21）
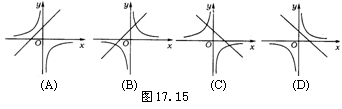15．已知一次函数y=k1x＋b，y随x的增大而减小，且b＞0；反比例函数y=
中的k2与k1值相等，则它们在同一坐标系中的图象只可能是( )
16．某同学在测量体温时意识到体温计的读数与水银柱的长度之间可能存在着某种函数关系，就利用体温计收集到的数据如下：
| 体温计的读数t（℃） | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| 水银柱的长度l（mm） | 56.5 | 62.5 | 68.5 | 74.5 | 80.5 | 86.5 | 92.5 | 98.5 |
请你根据上述数据分析判断，水银柱的长度l（mm）与体温计的读数t（℃）（
）之间存在的函数关系是（ ）
A. 
B. 
C.
D.
17．函数y＝
的自变量x的取值范围是 （ ）
A．–2<x≤1 B．x＞–2 C．–2≤x≤1 D．x＞–2且x≠3
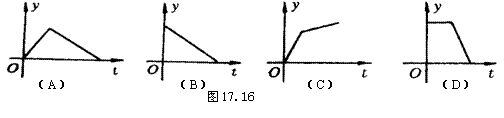18．（重庆市）某产品的生产流水线每小时可生产100件产品，生产前没有产品积压，生产3小时后安排工人装箱， 若每小时装产品150件，未装箱的产品数量(y)是时间(t)的函数，那么这个函数图象只能是( )
三、解答题（第19、20、21每题12分，第22、23每题15分，共66分）
19．已知一次函数y=(4m+1)x－(m+1)．
(1)m为何值时，y随x的增大而减小？
(2)m为何值时，直线与y轴的交点在x轴下方?
(3)m为何值时,直线位于第二、三、四象限?
20．已知y＋m与x＋n (m, n为常数)成正比例，判断y与x成什么函数关系；
若x=3时，y=5；x=5时，y=11，求出y与x之间的函数关系式．
21．如图17.17表示一艘轮船与一艘快艇沿
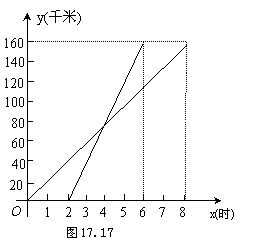相同路线从甲港到乙港行驶过程中路程随
时间变化的图象（分别是正比例函数图象
和一次函数图象）.根据图象解答下列问题：
(1)请分别求出表示轮船和快艇行驶过程的
函数解析式（不需写出自变量取值范围）；
(2)轮船和快艇在途中（不包括起点和终
点）行驶的速度分别是多少？
(3)问快艇出发多长时间赶上轮船？
22．(潍坊市，2004)（本小题满分１０分）
已知某山区的平均气温与该山的海拔高度的关系见下表：
| 海拔高度（单位：米） | 0 | １00 | ２00 | ３00 | ４00 | ．．． |
| 平均气温（单位：℃） | ２２ | 21.5 | ２1 | 20.5 | ２0 | ．．． |
(1)若海拔高度用（米）表示，平均气温用
（℃）表示，试写出与之间的函数关系式；
(2)若某种植物适宜生长在18℃～20℃(包含18℃,也包含20℃)山区,请问该植物适宜种植在海拔为多少米的山区?
23．某公司在甲、乙两座仓库分别有农用车12辆和6辆，现需要调往A县10辆，调往B县8辆．已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元；从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元．
(1)设从乙仓库调往A县农用车x辆，求总运费y关于x的函数关系式；
(2)若要让总运费不超过900元，问共有几种调运方案；
(3)求出总运费最低的调运方案，最低运费是多少？
第17章 综合能力测试答案
1．a＜0,b＜0（点拨：其图象分布在二、三、四象限，从而a＜0,b＜0．)
2．C（点拨：蓄水池的横断面是由“上大下小”的两个长方形构成．）
3．12，–2≤t≤14（点拨：4时气温最低(－2℃)；14时的气温最高(10℃)．）
4．A点坐标为(0,2)，B点坐标为(0,－4)．
5．Q=
aπD2，自变量是D，常量是aπ．
6．(3,4)或(3,–4)(点拨：MN∥y轴，则这两点的横坐标相等，N到x轴的距离为4，N的纵坐标为±4．)
7．1(点拨：设点P为(x1, y1),则S△POD=
=
=1．)
8．–3<a＜(点拨：点P在第四象限，则由3+a＞0，且2a－1＜0．)
9．11(点拨：函数y=2x+5的y随x的增大而增大，当x≥3时，y最小值=11．)
10．x<–1(点拨：因为y1>y2，则–2x–3>x．或直接利用函数的图象求解．)
11．A（关于x轴对称的两个点的的横坐标相等，纵坐标相反．）
12．D（点拨：正比例函数y=(3k—1)x的y随x的增大而增大，则3k—1＞0．）
13．A(点拨：1到5小时每小时所行的路程大小关系是：S1＞S2＞S3＞S4=S5=…=0，所以它们的速度关系是υ1＞υ2＞υ3＞υ4=υ5=…=0．所以②、③正确．)
14．C(点拨：先求出k=6,再确定只有点（－，－11）满足解析式y=6x－2．)
15．C（点拨：图C中，k1= k2<0，函数y=k1x＋b中y随x的增大而减小，函数y=的图象分布在二、四象限．）
16．C (点拨：设其函数关系式为l=6t-
，当t为35、36,l分别为56.5、62.5．)
17．A（点拨：函数y＝中x+2≥0,
≠0, 且1–x≥0．）
18．A （点拨：当时间0≤t≤3时，只生产不装箱，故未装箱的产品数量随时间的增加而增多，当t＞3时，生产量小于销售量，故未装箱的数量随时间的增加而逐步减少，故可同时排除B、C、D）．
19．(1) m＜－ (2) m＞－1时；(3)－1＜m＜－．
20．y+m与x + n成正比例，则y+m=k (x＋n) (k≠0)，整理得y=kx＋kn－m．
因为k≠0, m, n为常数，所以y是x的一次函数．
，(2)－(1)得2k=6, k=3，把k=3代入 (1)得kn－m=－4，即y=3x－4．
21．(1)轮船行驶过程的函数解析式y=20x，快艇行驶过程的函数解析式为y=40x－80；(2)轮船速度是
（千米/时），快艇速度
（千米/时）；(3)设快艇出发x小时赶上轮船，则20（x+2）=40x－80，解得：x=2．
22．(1)设与之间的函数关系式为y=kx+b,当x=0时y=22；当x=100时y=21.5，所以y=﹣0.005x+22，经检验，表中余下的三组数值均满足关系式y=﹣0.005x+22；(2) 解不等式组18≤﹣0.005x+22≤20,得400≤x≤800．故该植物适宜种植在海拔为400～800米的山区 ．
23．(1)设从乙仓库调往A县农用车x辆，则y=30x+50（6－x）+40（10－x）+80（2+x）．即y=20x+860．(2)因为总运费不能超过900，令20x+860≤900，得x≤2，由于x为非负整数，x的取值可为0，1，2，则共有三种调运方案．(3)当x=0时，y最小值=860(元)，即能得出总运费最低的调运方案与最低运费．