八年级数学下期末测试题（二）
班级___________ 姓名_____________.
考生注意：其中带※的题为升学考试要求而水平考试不要求的题目。
（总分：100分，考试时间：60分钟）
一、选择题（本大题8个小题，每小题4分，共32分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个答案是正确的，请选出填在题后的括号内。
1、若关于x的方程ax=3x-5有负数解，则a的取值范围是( )
A、a<3 B、a>3 C、a≥3 D、a≤3
2、一件工作，甲独做a小时完成，乙独做b小时完成，则甲、乙两人合作完成需要( )小时。
A、
B、
C、
D、
3、下列命题中假命题是（ ）
A、三个角的度数之比为1：3：4的三角形是直角三角形
B、三个角的度数之比为1：
：2的三角形是直角三角形
C、三边长度之比为1：：2的三角形是直角三角形
D、三边长度之比为
：：2的三角形是直角三角形
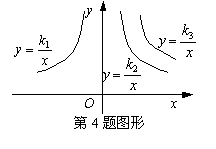
4、如图是三个反比例函数
，
，
在x轴上方的图象，由此观察得到
、
、
的大小关系为（ ）
A、 
B、 
C、 
D、 
 |
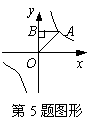5、如图，点A是反比例函数
图象上一点，AB⊥y轴于点B，则△AOB的面积是（ ）
A、1 B、2 C、3 D、4
6、在三边分别为下列长度的三角形中，哪些不是直角三角形（ ）
A、5，13，12 B、2，3，
C、4，7，5 D、1，
7、在下列性质中，平行四边形不一定具有的是（ ）
A、对边相等 B、对边平行 C、对角互补 D、内角和为360°
8、能判定四边形是平行四边形的条件是（ ）
A、一组对边平行，另一组对边相等 B、一组对边相等，一组邻角相等
C、一组对边平行，一组邻角相等 D、一组对边平行，一组对角相等
9、为了考查一批日光灯管的使用寿命，从中抽取了30 只进行试验，在这个问题中，下列说法正确的有（ ）
①总体是指这批日光灯管的全体 ②个体是指每只日光灯管的使用寿命
③样本是指从中抽取的30只日光灯管的使用寿命 ④样本容量是30只
A、1个 B、2个 C、3个 D、4个
10、当5个整数从小到大排列，则中位数是4，如果这5个数的唯一众数是6，则这5个整数可能的最大和是（ ）
A、21 B、22 C、23 D、24
※11、如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD的面积比是（ ）
A、3：4 B、5：8 C、9：16 D、1：2
 |
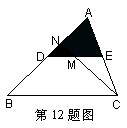
※12、如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于点N，则
△DMN∶四边形ANME
等于（ ）
A、1∶5 B、1∶4 C、2∶5 D、2∶7
二、填空题（本大题6个小题，每小题3分，共18分）在每小题中，请将答案直接写在题后横线上。
13、分式方程
+
的解是
。
14、若□ABCD中，AB=8，周长为24，则BC= ，CD= ，DA= 。
15、如图，□ABCD中，AE⊥CD于E，∠B=55°，则∠D= °，∠DAE= °。
 | |||
 | |||
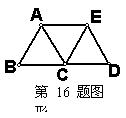16、如图，△ABC、△ACE、△ECD都是等边三角形，则图中的平行四边形有 。
17、将40cm长的木条截成四段，围成一个平行四边形，使其长边与短边的比为3:2，则较长的木条长 cm，较短的木条长 cm。
18、数据1，2，8，5，3，9，5，4，5，4的众数是_________；中位数是__________。
19、已知一个工人生产零件，计划30天完成，若每天多生产5个，则在26天完成且多生产15个。求这个工人原计划每天生产多少个零件?如果设原计划每天生产x个，根据题意可列出的方程为 。
20、若y与x成反比例，且图像经过点（-1，1），则y= 。（用含x的代数式表示）
21、如果一个三角形的三边a，b，c满足
，那么该三角形是
三角形。
22、已知，在△ABC中,AB＝1,AC＝,∠B=45°,那么△ABC的面积是
。
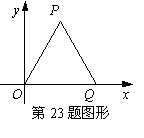
※23、如右图，△OPQ是边长为2的等边三角形，
若反比例函数的图象过点P，则它的解析式是_______。
※24、在四边形ABCD中，若已知AB∥CD，则再增加条件 即可使四边形ABCD成为平行四边形。
三、解答题（共50分）解答时请写出必要的演算过程或推理步骤。
25、（8分）计算：
。
26、（7分）在压力不变的情况下，某物承受的压强P（Pa）是它的受力面积S（m2）的反比例函数，其图象如右图所示。（1）求P与S之间的函数关系式；（2）求当S=0.5m2时物体所受的压强P。
27、（8分）如图，反比例函数
与一次函数
的图象交于A、B两点。（1）求A、B两点的坐标；（2）求△AOB的面积。
28、（7分）已知：如图，在□ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形。
求证：四边形ABOE、四边形DCOE都是平行四边形。
29、（8分）某校师生到距学校20千米的公路旁植树，甲班师生骑自行车先走，45分钟后，乙班师生乘汽车出发，结果两班师生同时到达，已知汽车的速度是自行车速度的2.5倍，求两种车的速度各是多少?
※30、（8分）如图，□ABCD中，BD⊥AD，AD=6cm，□ABCD的面积为24
，求□ABCD的周长及BD、AC的长。
※31、（10分）如图，□ABCD中，AE、CF分别是∠DAB、∠BCD的角平分线，你认为四边形AFCE是平行四边形吗？如果是，请说明理由。
※32、（10分）如图所示，一根长2a的木棍（AB），斜靠在与地面（OM）垂直的墙（ON）上，设木棍的中点为P。若木棍A端沿墙下滑，且B端沿地面向右滑行。
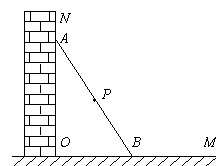（1）请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由。
（2）在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？简述理由，并求出面积的最大值。