八年级数学下学期期中测试题
（检测时间：120分钟 满分：120分）
班级：________ 姓名：_________ 得分：_______
一、选择题（3分×10分=30分）
1．医学研究发现一种新病毒的直径约为0.000043毫米，则这个数用科学记数法表示为（ ）
A．0.43×10-4 B．0.43×104 C．4.3×10-5 D．0.43×105
2．下列各组数中能够作为直角三角形的三边长的是（ ）
A．2，3，4 B．12，22，32 C．4，5，9 D．
，2，
3．下列各式从左到右变形正确的是（ ）
A．
+
=3（x+1）+2y B．
=
C．
=
D．
=
4．如果反比例函数的图象经过点（3，2），那么下列各点中在此函数图象上的点是（ ）
A．（-
，3） B．（9，
） C．（-
，2） D．（6，）
5．下列分式中与
的值相等的分式是（ ）
A．
B．
C．-
D．-
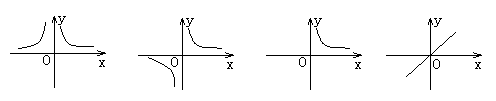6．如果矩形的面积为6cm2，那么它的长ycm与宽xcm之间的函数关系用图象表示大致是（ ）
A B C D
7．如图所示：数轴上点A所表示的数为a，则a的值是（ ）
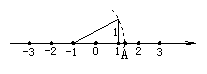A．
+1
B．-+1
C．-1
D．
8．“十一”旅游黄金周期间，几名同学包租一辆面包车前往“红螺寺”游玩，面包车的租价为180元，出发时，又增加了2名学生，结果每个同学比原来少分担3元车费，右参加游玩的同学为x人，则可得方程（ ）
A．
-
=2 B．-=3; C．-
=3
D．-=3
9．若xy=a，
+
=b（b>0），则（x+y）2的值为（ ）
A．b（ab-2） B．b（ab+2） C．a（ab-2） D．a（ab+2）
10．如图所示，已知∠1=∠2，AD=BD=4，CE⊥AD，2CE=AC，那么CD的长是（ ）
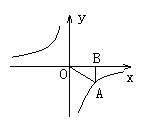A．2 B．3 C．1
D．1.5
(第10题) (第16题) (第20题)
二、填空题（3分×10=30分）
11．化简：
-
=________．
12．已知并联电路中的总电阻关系为
=
+
，那么R2=________（用R、R1表示）
13．“到一个角的两边距离相等的点，在这个角的平分线上”它的逆命题是_________．
14．已知a2-6a+9与│b-1│互为相反数，则式子（
-
）÷（a+b）的值为______．
15．若a+
=5，则a2+
=_________．
16．如图，一棵大树在一次强台风中于离地面3m处折断倒下，树干顶部在根部4米处，这棵大树在折断前的高度为_________．
17．近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知400度近视眼镜镜片的焦距为0.25m，则眼镜度数与镜片焦距之间的函数关系式为________．
18．已知点A（-2，a），B（-1，b），C（3，c）在双曲线y=
（k<0），则a、b、c的大小关系为________（用“〈”号将a、b、c连接起来〉．
19．已知反比例函数y=与一次函数y=2x+k的图象的一个交点的纵坐标是-4，则k的值是________．
20．如图所示，点A是反比例函数y=-
图象上一点，过点A作x轴的垂线，垂足为B点，若OA=2，则△AOB的周长为________．
三、计算（9分）
21．（1）（-2ab）÷
·
; （2）（a-
）÷
·
;
（3）
-
÷
.
四、解方程（4分）
22．（1）
+
=0．
（2）
=1-
.
五、解答题（5分，5分，6分，7分，5分，6分，9分，计43分）
23．先化简，再求值:
-
，其中x=2．
24．已知：a2+a-1=0，求分式
的值．
25．如图，一次函数y=ax+b的图象与反比例函数y=的图象交于M、N两点．
（1）利用图中条件，求反比例函数和一次函数的解析式；
（2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围．
 |
26．某服装店用960元购进一批服装，并以每件46元的价格全部售完，由于服装畅销，服装店又用2220元，再次以比第一次进价多5元的价格购进服装，数量是第一次购进服装的2倍，仍以每件46元的价格出售，卖了部分后，为了加快资金周转，服装店将剩余的20件以售价的九折全部出售．问：
（1）该服装店第一次购买了此种服装多少件？
（2）两次出售服装共盈利多少元？
27．已知，如图四边形ABCD中，∠B=90°，AB=4，BC=3，AD=13，CD=12，求：四边形ABCD的面积．
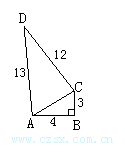
28．若a、b、c是△ABC的三边长，且满足a2c2-b2c2=a4-b4，试判定这个三角形的形状．
29．大小两种货车运送360台机械设备，有三种运输方案．
方案一：设备的
用大货车运送，其余用小货车运送，需要货车27辆．
方案二：设备的
用大货车运送，其余用小货车运送，需要货车28辆．
方案三：设备的用大货车运送，其余用小货车运送，需要货车26辆．
（1）每辆大、小货车各可运送多少台机械设备？
（2）如果大货车运费比小货车高m%（m>0），请你从中选择一种方案，使得运费最低，并说明理由．
答案:
1．C 2．D 3．C 4．B 5．B 6．C 7．D 8．A 9．D 10．A
11．
12．
13．略 14． 15．23 16．8 17．y=
18．c<a<b
19．-8
20．6+2
21．（1）
；（2）；（3）-
22．（1）x=；（2）x=3
23．2x-1，3 24．-5
25．（1）y=
，y=2x-2；（2）x<-1或0<x<2
26．（1）第一次30件，第二次60件；（2）868元
27．36
28．解：a2c2-b2c2=a4-b4，∴a2c2-b2c2-a4+b4=0．
∴c2（a2-b2）-（a2+b2）（a2-b2）=0．
∴（a2-b2）（c2-a2-b2）=0．
∴a2-b2=0或c2-a2-b2=0．
∴a=b或a2+b2=c2．
∴△ABC为等腰三角形或直角三角形．
29．（1）设大货车有x辆，每辆装有机器台，小货车有（27-x）辆，
每辆装有机器
台，依题意得方程
+
=28，解得x=12，
小货车为27-12=15（辆），大货车每辆装15台，小货车每辆装12台，
（2）设小货车每台每次运费a元，
方案一：w1=（27+12m%）a，
方案二：w2=（28+8m%）a，
方案三：w3=（26+16m%）a，
当0<m%<25%，∴w3<w1<w2，方案三运费最低．
当m%=25%时，w1=w2=w3三种方案运费一样，
当m%>25%时，w2<w1<w3方案二运费最低.