八年级数学上学期期末质检
数 学 试 卷
(完卷时间：120分钟；满分：100分)
一、选择：(选一个正确答案的代号填入括号内，每小题2分，共20分)
1、下列各式中运算结果为x8的是( )
A、x4·x4； B、(x4)4； C、x16÷x2； D、x4＋x4．
2、下列计算中，正确的是( )
A、2a＋3b＝5ab； B、a3－a2＝a； C、a2＋2a2＝3a2； D、(a－1)0＝1．
3、为了反映某地某日的气温变化情况，最好选择(
)
A、条形统计图； B、折线统计图； C、扇形统计图； D、直方图．
4、如图，△ABC是不等边三角形，现以B、C为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以作( )
A、2个； B、3个； C、4个； D、5个．
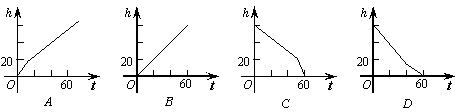
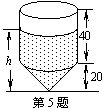5、如图是一个蓄水桶，60分钟可将一满桶水放干．现此桶装满水，那么在放水过程中，水位h(cm)随放水时间t(分钟)变化的大致图象为(
)
 |
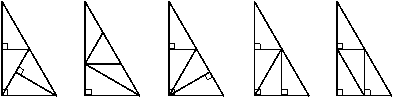6、有一个含有60°角的直角三角形绿化地带，现要求把它分成四个面积相等、形状完全相同的三角形地块，准备种植四种不同的花卉．某同学提供了如图所示的五种设计方案，其中可以满足要求的有( )
A、2种； B、3种； C、4种； D、5种．
7、下图的四个图案中，与众不同的一个是(图中黑色图形的顶点都在小正方形的顶点上)( )
 |
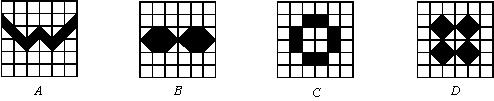8、已知一次函数y＝kx＋b(k≠0)的图象与坐标轴的交点分别为(－1，0)和(0，－2)，则不等式kx＋b＜0的解集是( )
A、x＞－2； B、x＜－2； C、x＞－1； D、x＜－1．
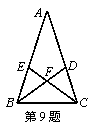
9、如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是∠ABC与∠ACB的角平分线，且相交于点F，则图中的等腰三角形共有( )
A、6个； B、7个； C、8个； D、9个．
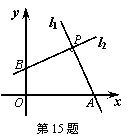
10、某校八年级同学到距学校6千米的郊外春游，如图的l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象，则以下判断错误的是( )
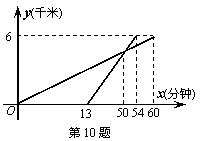A、步行的速度是6千米/时；
B、骑车的速度是15千米/时；
C、骑车的同学比步行的同学先到达目的地6分钟；
D、骑车的同学用了30分钟追上了步行的同学．
二、填空：(每小题3分，共15分)
11、分解因式：a3b－ab＝___________________．
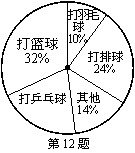
12、如图是八年(1)班同学在活动课时参加各种活动的统计图，则打乒乓球的部分所对的圆心角是______________．
13、有的汉字在水中的倒影与原来的字一样，如“日、目、回、王”等．请你再写出3个这样的汉字________________________．
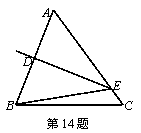
14、如图，△ABC中，BC＝8cm，AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长为18cm，则AC的长为_____________cm．
15、如图，P点坐标为(3，3)，l1⊥l2，l1、l2分别交x轴和y轴于A点和B点，则四边形OAPB的面积为_________________．
 | |||||
 | |||||
 | |||||
三、(每小题4分，共12分)
16、因式分解：3x3－12x2y＋12xy2．
17、计算：x·x3＋(－2x2)2＋24x6÷(－4x2)．
18、计算：(2a－3b)(3b＋2a)－(8a3b－6ab3)÷2ab．
四、(每小题5分，共10分)
19、先化简，再求值：[(x＋2y)2－2y(x＋2y)－8xy]÷2x，其中x＝－4，y＝1．
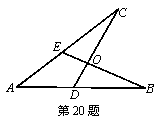20、如图，下面四个条件中，请你选择三个条件，以其中两个作为已知条件，另一个为结论，写出一个正确的命题(只需写出一种情况)，并加以证明．
① AE＝AD； ② AB＝AC； ③ OB＝OC； ④ ∠B＝∠C．
已知：
求证：
证明：
五、(每小题6分，共24分)
21、如图所示，已知B(1，－2)，C(3，0)．
(1) 试确定A点坐标，使△ABC关于x轴成轴对称图形，并连接AB、AC；
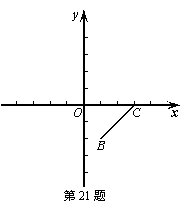(2) 作出△ABC关于y轴的对称图形A'B'C'(不写作法)，并写出A'、B'、C'的坐标．
22、为了了解学生参加体育活动的情况，某校随机抽样调查了200名学生，其中一个问题是“你平均每天参加体育活动的时间是多少？”共有4个选项：
A、1.5小时以上； B、1~1.5小时； C、0.5~1小时； D、0.5小时以下．
如图是根据调查结果绘制的两幅不完整的统计图，请你结合统计图提供的信息，解答以下问题：
 |
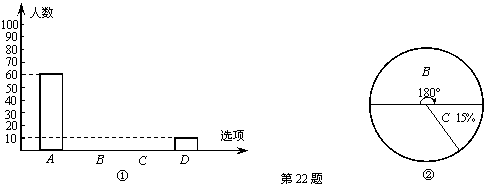(1) 在图①中将选项“B”“C”的部分补充完整；
(2) 补全图②中的扇形统计图；
(3) 若该校有3000名学生，你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下？
23、已知在△ABC中，AB＝AC，∠BAC＝120°，AC的垂直平分线EF交AC于点E，交BC于点F，试判断BF与CF有什么数量关系？并说明理由．
 |
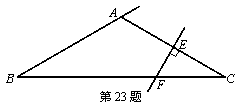24、阅读：我们刚学过完全平方公式(a＋b)2＝a2＋2ab＋b2，当a＞0，b＞0时，用面积说明公式成立的方法如下：
如图(1)，把一个边长为(a＋b)的正方形按如图所示的方法分割成四块，则四块的面积分别为a2、ab、ab、b2，依图可得(a＋b)2＝a2＋ab＋ab＋b2＝a2＋2ab＋b2．
问题：如图(2)中的正方形边长为(a＋b＋c)，请用以上类似的方法，先对正方形进行适当的分割，再依图求出(a＋b＋c)2的结果．
 |
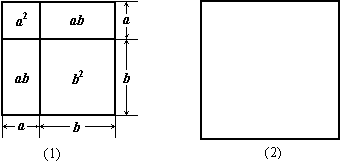六、(25题8分，26题11分，共19分)
25、(1) 如图①，△ABC是等边三角形，D是AB上一点，以CD为一边向上作等边△ECD，连接AE，求证：∠CAE＝∠CBA．
(2) 在上题(1)中，当D点在AB的延长线上时，其他条件不变，如图②所示，请你补画出题意的图形，(1)的结论还成立吗？若成立，请给予证明；若不成立，请简要说明理由．
 |
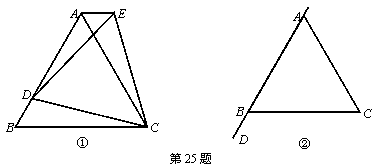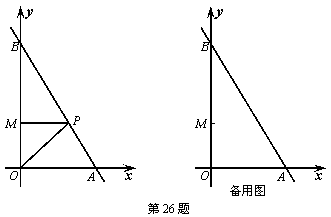
26、如图，已知直线AB与x轴交于A(6，0)点，与y轴交于B(0，10)点，点M的坐标为(0，4)，点P(x，y)是折线O→A→B的动点(不与O点、B点重合)，连接OP、MP，设△OPM的面积为S．
(1) 求S关于x的函数表达式，并求x的取值范围；
(2) 当△OPM是以OM为底边的等腰三角形时，求S的值；
(3) 当线段MP分△OAB的面积比为1∶4时，求P点坐标．
 |
数 学 试 卷
参考答案：
一、
1、A；2、C；3、B；4、B；5、C；6、C；7、A；8、C；9、C；10、D。
二、
11、ab(a＋1)(a－1)；12、72°；13、略；14、10；15、9。
三、
16、3x(x－2y)2；17、－x4；18、－6b2。
四、
19、0.5x－3y；－5；20、略。
五、
21、(1) A(1，2)；图略；(2) A'(－1，2)、B'(―1，―2)、C'(－3，0)。
22、(1) 略；(2) 略；(3) 150人。
23、BF＝2CF；证明略。
24、图略；(a＋b＋c)2＝a2＋b2＋c2＋2ab＋2bc＋2ca。
25、(1) 证明略；(2) 不成立。
26、(1) S＝2x (0＜x≤6)；(2) S＝9.6；(3) P(3，0)或P(2，
)。