八年级数学4月份月考试题
满分:100分 考试时间:120分钟
一.细心填一填:(每小题2分,共20分)
1.当![]() = 时,分式
= 时,分式![]() 的值为0.
的值为0.
2.纳米是一种长度单位,1纳米=![]() 米,已知某植物的花粉的直径约为3500纳米,那么用科学记数法表示该花粉的直径为
米.
米,已知某植物的花粉的直径约为3500纳米,那么用科学记数法表示该花粉的直径为
米.
3.已知函数![]() 是反比例函数,则
是反比例函数,则![]() = .
= .
4.已知反比例函数![]() ,当x=6,y=8时,则m
= .
,当x=6,y=8时,则m
= .
5.方程![]() 的解是
.
的解是
.
6.在函数![]() 中,自变量x的取值范围是
.
中,自变量x的取值范围是
.
7.若点A(7,![]() )、B(5,
)、B(5,![]() )在双曲线
)在双曲线![]() 上,则
上,则![]() 和
和![]() 的大小关系为_________.
的大小关系为_________.
8.化简![]() .
.
9.当![]() = 时,关于
= 时,关于![]() 的方程
的方程![]() 会产生增根.
会产生增根.
10.已知![]() 的值随x的增大而增大,则函数
的值随x的增大而增大,则函数![]() 的图象在 象限.
的图象在 象限.
二.精心选一选(每小题3分,共18分)
11.下列各式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,是分式的共有( )
中,是分式的共有( )
A.1个 B.2个 C.3个 D.4个
12.下列各式与![]() 相等的是( ).
相等的是( ).
A.![]() B.
B. 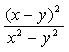 C .
C . ![]() D.
D.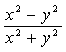
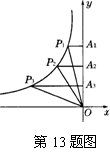 13.如图,
13.如图,![]() 是双曲线上的三点.过这三点分别作y轴的垂线,得到三个三角形
是双曲线上的三点.过这三点分别作y轴的垂线,得到三个三角形![]() 、
、![]() 、
、![]() ,设它们的面积分别是
,设它们的面积分别是![]() ,则( ).
,则( ).
A.S1=S2=S3 B. S2<S1<S3
C.S1<S3<S2 D. S1<S2<S3
14.函数![]() 的图象上有两点
的图象上有两点![]() 、
、![]() 且
且![]() ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 与
与![]() 之间的大小关系不能确定
之间的大小关系不能确定
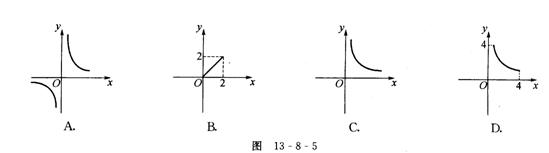 15.如图13-8-5,面积为2的ΔABC,一边长为
15.如图13-8-5,面积为2的ΔABC,一边长为![]() ,这边上的高为
,这边上的高为![]() ,则
,则![]() 与
与![]() 的变化规律用图象表示大致是 ( )
的变化规律用图象表示大致是 ( )
16. 在同一平面直角坐标系中,函数y=k(x-1)与y=![]() 的大致图象是( )
的大致图象是( )

A B C D
三.耐心做一做(共62分)
17.计算(每小题4分,16分)
(1)![]()
(2)![]() (3)
(3)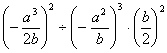
(4)先化简下式,再对x选取一个使原式有意义,而你又喜欢的数代入求值:
![]()
18.解方程(每小题5分,共10分)
(1)![]() (2)
(2)![]()
19.列分式方程解应用题(7分)
某开发公司的960件新产品需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的![]() ,问甲、乙两工厂每天各能加工多少件新产品?
,问甲、乙两工厂每天各能加工多少件新产品?
20.(5分)已知![]() 与
与![]() 成反比例,并且
成反比例,并且![]() =6时,
=6时,![]() =7
=7
(1)求![]() 与
与![]() 的函数关系式;(2)当
的函数关系式;(2)当![]() 时,
时,![]() 的值是多少?
的值是多少?
(3)当![]() =3时,
=3时,![]() 的值是多少?
的值是多少?
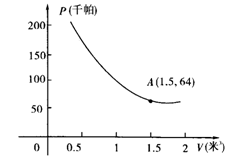
21.(6分)某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
(1) 写出这个函数的解析式;
(2) 当气球的体积为0.8立方米时,气球内的气压是多少千帕?
(3) 当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米。
22.(4分)先阅读下面的材料,然后解答问题:
通过观察,发现方程
![]() 的解为
的解为![]() ;
; ![]() 的解为
的解为![]() ;
;
![]() 的解为
的解为![]() ; …………………………
; …………………………
(1)
观察上述方程的解,猜想关于x的方程![]() 的解是________________;
的解是________________;
(2)
根据上面的规律,猜想关于x的方程![]() 的解是___________________;
的解是___________________;
(3) 把关于x的方程![]() 变形为方程
变形为方程![]() 的形式是______
__,方程的解是_________
_.
的形式是______
__,方程的解是_________
_.
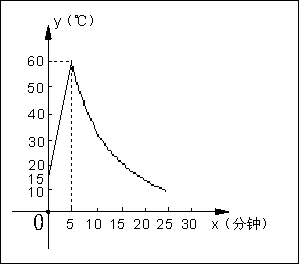
23.(7分)制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃. (1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
24.(7分)某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20米和11米的矩形大厅内修建一个64平方米的矩形健身房ABCD。该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/平方米,新建(含装修)墙壁的费用为80元/平方米。设健身房的高为3米,一面旧墙壁AB的长为x米,修建健身房的总投入为y元。
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足8≤x≤12.当投入资金为4800元时,问利用旧墙壁的总长度为多少米?

参考答案:
一.细心填一填:(每小题2分,共20分)
1.3 ; 2. ![]() ; 3. 1 ; 4. 24 ; 5. x = 5 ; 6.
; 3. 1 ; 4. 24 ; 5. x = 5 ; 6. ![]() ;
;
7.![]() ; 8.
; 8.![]() ; 9. 6
;10. 二、四 .
; 9. 6
;10. 二、四 .
二.精心选一选(每小题3分,共18分)
11`16 C B A D C B
三.耐心做一做(共62分)
17.(1)-4 (2)![]() (3)
(3)![]() (4)
(4)![]()
18.(1)x = -4 (2)无解 19. 16,24
20.(1)![]() (2)18 (3)14
(2)18 (3)14
21.(1)![]() (2)120
(3)
(2)120
(3)![]()
22.(1)![]() (2)
(2)![]()
(3)![]() ;
; ![]()
23. (1)![]()
![]() (2)20分钟
(2)20分钟
24.(1)根据题意,AB = x,AB·BC=60,所以![]() .
.
![]() ,即
,即![]() .
.
(2) 当y=4800时,有![]() 得x=8 符合题意
得x=8 符合题意
所以利用旧墙壁的总长度为![]() 米.
米.