八年级数学上册期末复习测试二
一、选择题（每题2分，共24分）
1、计算
的结果是（ ）
A、
B、
C、
D、
2、某服装销售商在进行市场占有率的调查时，他最应该关注的是（ ）
A. 服装型号的平均数 B. 服装型号的众数 C. 服装型号的中位数 D. 最小的服装型号
3、已知一直角三角形的木板，三边的平方和为1800cm2,则斜边长为（ ）.
A、80cm B、30cm C、90cm D、120cm.
4、若点（
）、
、
都在反比例函数
的图象上，则
的大小关系是
A、
B、
C、
D、
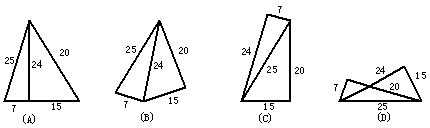
5、五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ）
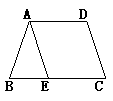
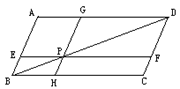
6、如图，等腰梯形ABCD中，AD∥BC，AE∥DC，∠B=60º，BC=3，△ABE的周长为6，则等腰梯形的周长是 （ ）
A 、8
B 、10 C、12 D、16
（第6题） （第9题） （第12题）
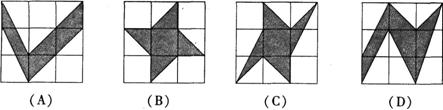
7、在下面图形中，每个大正方形网格都是由边长为1的小正方形组成，则图中阴影部分面积最大的是( )
8、若关于
的方程
有增根，则
的值是
A．－2 B．2 C．5 D．3
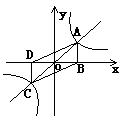
9、正比例函数y=x与反比例函数y=
的图象相交于A、C两点.AB⊥x轴于B,CD⊥y轴于D(如图),则四边形ABCD的面积为( )
A.1 B.
C.2
D.
10、某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛，随机抽取甲、乙两名车工加工的5个零件，现测得的结果如下表，请你用计算器比较S 2甲、S 2乙的大小（ ）
| 甲 | 10.05 | 10.02 | 9.97 | 9.96 | 10 |
| 乙 | 10 | 10.01 | 10.02 | 9.97 | 10 |
A．S 2甲＞S 2乙 B．S 2甲＝S 2乙 C．S 2甲＜S 2乙 D．S 2甲≤S 2
11、某市为处理污水需要铺设一条长为4000米的管道，为了尽量减少施工对交通所造成的影响，实际施工时每天比原计划多铺设10米，结果提前20天完成任务。设原计划每天铺设管道x米，则可得方程（ ）
A、
B、
C、
D、
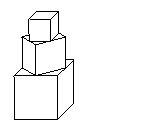
12、若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是 （ ）
A、2 B、3 C、4 D、5
二、填空题（每题2分，共24分）
13、如果反比例函数的图象经过点（1，-2），那么这个反比例函数的解析式为_______
14、不改变分式的值，把下列各式分子与分母中各项的系数都化为整数且使各项系数最小：
（1）
=
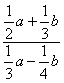； （2）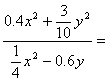
。
15、单位举行歌咏比赛，分两场举行，第一场8名参赛选手的平均成绩为88分，第二场4名参赛选手的平均成绩为94分，那么这12名选手的平均成绩是 分
16、若a＝
，
的值等于_______.
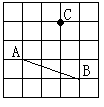
17、如图是某广告公司为某种商品设计的商标图案，若图中每个小长方形的面积都是1，则阴影部分的面积是______
（第17题） （第18题） （第19题）
18、如图，在菱形ABCD中，∠ABC=60°，E为AB边的中点，P为对角线BD上任意一点，AB＝4，则PE＋PA的最小值为__________________.
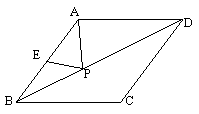
19、如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，图中面积相等的四边形共有____________对。
20、已知
＝3，则分式
的值为_______
21、如图，将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E，使DE=5，这痕为PQ，则PQ的长为_______
（第22题） （第24题）
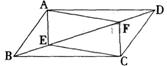
22、如图，E、F是
ABCD对角线BD上的两点，请你添加一个适当的条件：
，使四边形AECF是平行四边形．
23、已知x为整数，且
为整数，则所有符合条件的x的值的和是____________。
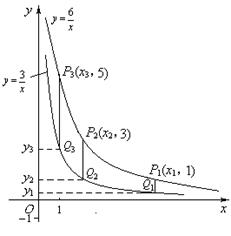
24、两个反比例函数
，
在第一象限内的图象如图所示, 点P1，P2，P3，…，P2 005在反比例函数图象上，它们的横坐标分别是x1，x2，x3，…，x2
005，纵坐标分别是1，3，5，…，共2
005个连续奇数，过点P1， P2，P3，…，P2 005分别作y轴的平行线，与的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2 005（x2 005，y2 005），则y2 005= ．
三、解答题（共52分）
25、（4分）当
时，求
的值。
26、（4分）请你阅读下列计算过程，再回答所提出的问题：
题目计算
解：原式=
（A）
=
（B）
=x-3-3(x+1) （C）
=-2x-6 （D）
（1）上述计算过程中，从哪一步开始出现错误：_______________
（2）从B到C是否正确，若不正确，错误的原因是__________________________
（3）请你正确解答。
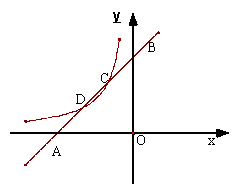27、（4分）如图，已知直线
与轴、
轴分别交于点A、B，与双曲线
（<0）分别交于点C、D，且C点的坐标为（
，2）.
⑴分别求出直线AB及双曲线的解析式；
⑵求出点D的坐标；
⑶利用图象直接写出：当x在什么范围内取值时，
>
.
28、（6分）已知函数y = y1－y2，y1与x成反比例，y2与x－2成正比例，且当x = 1时，y =－1；当x = 3时，y = 5.求当x＝5时y的值。
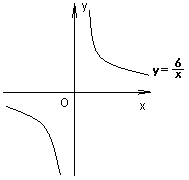29、（6分）若反比例函数
与一次函数
的图象都经过点A（
，2）
（1）求点A的坐标；
（2）求一次函数的解析式；
（3）设O为坐标原点，若两个函数图像的另一个交点为B，
求△AOB的面积。
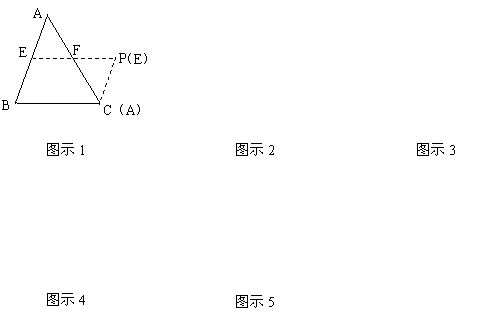
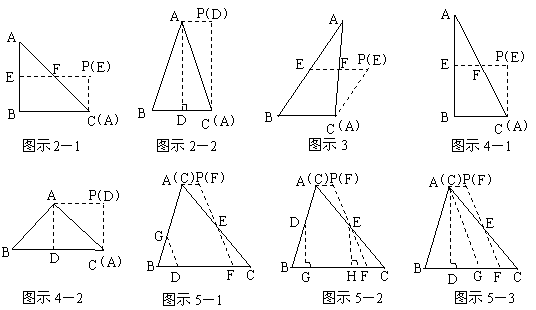
30、（12分）在△ABC中，借助作图工具可以作出中位线EF，沿着中位线EF一刀剪切后，用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP，剪切线与拼图如图示1，仿上述的方法，按要求完成下列操作设计，并在规定位置画出图示，
⑴在△ABC中，增加条件＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成矩形，剪切线与拼图画在图示2的位置；
⑵在△ABC中，增加条件＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成菱形，剪切线与拼图画在图示3的位置；
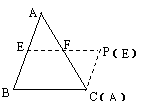⑶在△ABC中，增加条件＿＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成正方形，剪切线与拼图画在图示4的位置
⑷在△ABC（AB≠AC）中，一刀剪切后也可以拼成等腰梯形，首先要确定剪切线，其操作过程（剪切线的作法）是：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
然后，沿着剪切线一刀剪切后可以拼成等腰梯形，剪切线与拼图画在图示5的位置.
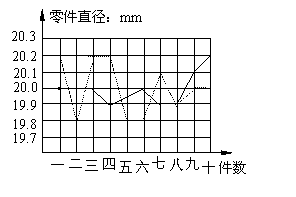
31、（6分）为选派一名学生参加全市实践活动技能竞赛，A、B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试，他俩各加工的10个零件的相关数据依次如下图表所示（单位：mm）
根据测试得到的有关数据，试解答下列问题：
⑴ 考虑平均数与完全符合要求的个数，你认为 的成绩好些；
⑵ 计算出SB2的大小，考虑平均数与方差，说明谁的成绩好些；
⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由。
| 平均数 | 方差 | 完全符合要求个数 | |
| A | 20 | 0.026 | 2 |
| B | 20 | SB2 |
 |
32、（10分）已知，点P是正方形ABCD内的一点，连PA、PB、PC.
（1）将△PAB绕点B顺时针旋转90°到△P′CB的位置（如图1）.
①设AB的长为a，PB的长为b（b<a），求△PAB旋转到△P′CB的过程中边PA所扫过区域（图1中阴影部分）的面积；
②若PA=2，PB=4，∠APB=135°，求PC的长.
（2）如图2，若PA2+PC2=2PB2，请说明点P必在对角线AC上.
 |
参考答案：
一、选择题
1、A 2、B 3、B 4、D 5、C 6、A 7、D 8、D 9、C 10、A 11、D 12、B
二、填空题
13、
14、
，
15、90 16、
17、
18、
19、5对
20、
21、13 22、BE＝DF 23、12 24、2004.5
三、解答题
25、
，2
26、（1）A到B
（2）不正确，不能去分母
（3）＝
＝
＝
27、（1）
，
，（2）（－2，1）（3）
28、解：设
，
，则y = 
。
根据题意有：
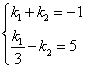，解得：
，
∴
当x＝5时,y
=
.
29、（1）点A的坐标（3，2）（2）
（3）△AOB的面积为8。
30、⑴ 方法一：∠B＝90°，中位线EF，如图示2－1.
方法二：AB＝AC，中线（或高）AD，如图示2－2.
⑵ AB＝2BC（或者∠C＝90°，∠A＝30°），中位线EF，如图示3.
⑶ 方法一：∠B＝90°且AB＝2BC，中位线EF，如图示4－1.
方法二：AB＝AC且∠BAC＝90°，中线（或高）AD，如图示4－2.
⑷ 方法一：不妨设∠B＞∠C，在BC边上取一点D，作∠GDB＝∠B交AB于G，过AC的中点E作EF∥GD交BC于F，则EF为剪切线.如图示5－1.
方法二：不妨设∠B＞∠C，分别取AB、AC的中点D、E，过D、E作BC的垂线，G、H为垂足，在HC上截取HF＝GB，连结EF，则EF为剪切线.如图示5－2.
方法三：不妨设∠B＞∠C，作高AD，在DC上截取DG＝DB，连结AG，过AC的中点E作EF∥AG交BC于F，则EF为剪切线.如图示5－2.
31、（1）B (2)B（3）B呈现上升趋势
32、（1）①S阴影=
②连结PP′，证△PBP′为等腰直角三角形，从而PC=6;
（2）将△PAB绕点B顺时针旋转90°到△P′CB的位置，由勾股逆定理证出∠P′CP=90°，再证∠BPC+∠APB=180°，即点P在对角线AC上.