八年级数学上学期月考试题

八年级数学上学期月考试题

一、选择题：（3×10）

1．如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是（　　 ）

A、同位角　　B、内错角　 C、对顶角　 D、同旁内角

（1）

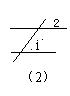
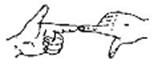
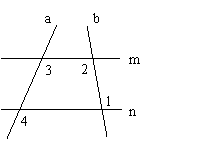
2.如图，直线a//b，∠1=40⁰，∠2的度数为---------------------------------（　　 ）

A  140⁰　　　B　50⁰ 　　C　40⁰　　　 D 100⁰

3．已知等腰三角形的两边长分别为4、9，则它的周长为（　　　）

（A）17　 （B）22　 （C）17或22　 （D）13

4．如果∠α和∠β是同位角，且∠α=55°则∠β等于　　（　　　 ）

A．55°　　B。125°　 C。55°或125°　　D。无法确定

5．下列图形中，不一定是轴对称图形的是　 （　　　）

A．线段　 B．角　 C．直角三角形　 D．等腰三角形

6．3、 以下列三个数为边长的三角形能组成直角三角形的是 （　 　）

　 A　 1, 1 ,2　　B　 5, 8 10　　 C　6 ,7 ,8　 D　3 ,4 ,5

7．下列能断定△ABC为等腰三角形的是（　　　）

（A）∠A=30º、∠B=60º　　　　（B）∠A=50º、∠B=80º

（C）∠A=30º、∠B=80º　　　　（D）∠A=50º、∠B=70º

8．等腰三角形的顶角等于70^o，则它的底角是　　(　　 )

A、70^o　　　　　　B、55^o　　 　　　　C、　 60^o　　　　D、 70^o或55^o

9．下列说法正确的是（　　  ）

　A．同位角相等B．内错角相等C．对顶角相等 D．同旁内角互补

10．已知等腰△ABC的底边BC=8cm，且│AC-BC│=2cm，那么腰AC的长为（  ）

　　A．10cm或6cm　　B、10cm　　C、6cm　　D、8cm或6cm

二、填空题：（3×10）

1．如图，直线a∥b，∠1=130°，则∠2=　　　 度．

2．在等腰三角形ABC中，AB=AC，若∠B=40°，则∠A=　　　，∠C=

　　　  。

3．等边三角形有　　　条对称轴。

4．Rt⊿ABC的斜边长为6cm,则斜边上的中线长为　　　cm.

5. 在Rt△ABC中,∠C=90度,∠B=25度,则∠A=______度.

6．如图，若AD∥BC，AB∥DC，∠A=63°，则∠C=  　　 。

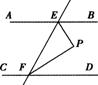
7．已知：如图， AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DEF的平分线相交于点P。∠P=  　　．

(第7题)

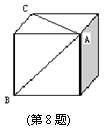
8.如图，在一个正方体的两个面上画了两条对角线AB，AC，那么这两条对角线的夹角

等于　 　度.

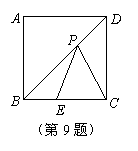
9.在正方形ABCD中，点E是BC上的一定点，且BE=10，EC=14,

点P是BD上的一动点，则PE+PC的最小值是　　　　　　　  ．

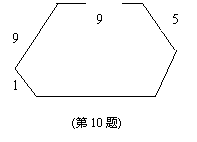
10．.如图,一个六边形的6个内角都是120°,其连续四边的长依次是1、9、9、5（cm），那么这个六边行的周长是　　　　。

养真中学八年级数学月考试题

2007　 年　 10　 月

一、选择题：（3×10）

1．　　 、2．　　 、3．　　　、4．　　　、5．　　　、

6．　　 、7.　　　、8．　　　、9．　　　、10.　　　 。

二、填空题：（3×10）

1.　　　 、2.　　　 、　　　　、3.　　　 、4.　　　　、5.　　　 、

6.　　　  、7.　　　 、8.　　　　 、9.　　　　、10.　　　　

三．解答题（60分）

21．（7分）如图，∠1=100°，∠2=100°，∠3=120°，填空：（5分）

∵∠1=∠2=100°（已知）

∴　　　　∥　　　 （　　　　　　　　　　　　  ）

∴∠　　　=∠　　　（　　　　　　　　　　　　  ）

又∵∠3=120°（已知）

∴∠4=　　　　 度

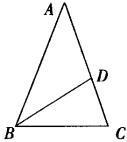
22．（7分）如图，已知：在 中， ，∠A=40° ，BD是 的角平分线，求 的度数.(写清解题过程)

23．（8分）如图，已知∠EAC是△ABC的外角，∠1=∠2，AD∥BC，请说明AB=AC的理由。

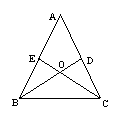
24．（8分）如图，中，AB=AC，2条角平分线BD、CE相交于点O。

OB与OC相等吗？请说明你的理由；

D

C

25．（8分）如图，△ABC和△ABD中，AC⊥BC，AD⊥BD，E是AB边上的中线。试判断DE与CE是否相等，并说明理由。

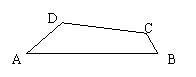
26、（6分）如图，在四边形ABCD中，AB=8，BC=1，∠DAB=30°，∠ABC=60°，四边形ABCD的面积为5，求AD的长。

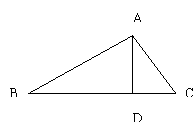
27. （6分）如图，△ABC中，AD⊥BC于D,∠C=2∠B,说明AC+CD=BD的理由。