八年级数学上月考试卷
| 题 号 | 一 | 二 | 三 | 四 | 五 | 总 分 |
| 得 分 |
|
|
|
|
|
|
一、选择题：（每题3分，共24分）
1、一元一次不等式组
的解集为x>a，且a≠－1，则a取值范围是（ ）。
A、a>－1 B、a<－1 C、a>0 D、a <0
2、下列各对不等式 (1)3x≤9与x≤－3；(2)2x－7≤6x与4x≤－7；
(3)－4x<12与x>－3；(4)3.14x<0与x<0其中解相同不等式的是（ ）。
A、(1)(2) B、(2)(4) C、(1)(4) D、(3)(4)
3、－
的值是非负数，则x的取值范围是（ ）。
A、x≤－1 B、x≥－1 C、x≥1 D、x≤1
4、要使代数式
有意义，则x的取值范围是（ ）。
A、x≤
且x≠0 B、x>－
且x≠0 C、x≠0 D、x<且x≠0
5、点P（1，2）关于x轴的对称点在第（ ）象限。
A．一 B．二 C．三 D．四
6、将△ABC的3个顶点坐标的纵坐标乘以－1，横坐标不变，则所得图形与原图形的关系是（ ）。
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．将原图向x轴的负向平移了1个单位
7、将点M（a，b）关于y轴的对称点，向上平移3个单位，所得的像的坐标是（ ）。
A．（a－3，－b） B．（ a+3，b） C．（－a，b－3）D．（－a，b+3）
8、右图，是跳棋盘，格点上的黑色点为棋子，我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿着棋子对称跳行，跳行一次称为一步，已知点A为己方一枚棋子，欲将棋子A跳进对方区域(阴影部分的格点)，则跳行的最少步数为___________步。
A．1 B．2 C．3 D．4
二、填空题：（每题3分，共24分）
9、给出下列不等式：
①;②
；③3x－y<5; ④
⑤x≤0
其中属于一元一次不等式的是： （只填序号）
10、满足不等式4x－4＜6 x－3的解集是
11、P（10，a），Q（b，－20）关于y轴对称，则a=_________，b=________．
12、点A在x轴上方，距x轴4个单位长度，距y轴3个单位长度，则A点的坐标是 ，A点离开原点的距离是_ ___。
13、如图，如果（士）所在位置的坐标为(－1,0), （相）所在位置的坐标为(2,0), 那么，（炮）所在位置的坐标为
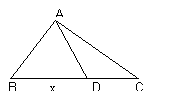
14、如右图，△ABC边长BC是10，BC边上的高是 6,D点在BC上运动，设BD长为x,△ABD的面积为y，用x的代数式表示 y，则y=
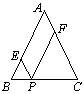
15、如右图：在△ABC中：AB=AC=6cm,P是BC边上任一点，PE∥AC，PF∥AB，
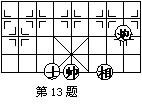则四边形AEPF的周长
cm。
第
第14题 第15题
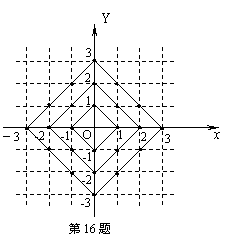
16、在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点. 观察图中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点个数共有_________个.
三、解答题（共52分）
17、（6分）
解不等式组，把解集表示在数轴上。
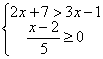
18、（6分）已知三角形三边长分别为3，（1－2x），8，试求x的取值范围。
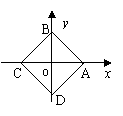19、（6分） 如图，已知坐标系中的正方形ABCD的边长为4, 求其各个顶点的坐标。
20、（6分）学生若干人分住在若干间宿舍，如果每间宿舍住4人，那么有20人没有宿舍住；如果每间宿舍住8人，那么有一间宿舍不空也不满。求学生的人数和宿舍的间数。
21、（6分）小王同学想知道学校旗杆的高，他发现从旗杆顶上挂下来的绳子垂直到地面还多1米（如图），当他把绳子拉开离
旗杆底部5米后，绳子下端刚好接触地面；请你帮小王
同学算一算学校旗杆高度．
22、（6分）观察下列“小鱼”图案，并回答下列问题：
（1） 分别求出“小鱼”图案各个顶点所对应的坐标；
（2） 画出“小鱼”以y轴为对称轴作轴对称变换以后的图形，并写出所得图象各顶点的坐标；
（3） 
把第（2）题所得的图象先向左平移1个单位，再向下平移4个单位，并画出经变换后所得的图象。
Y
X
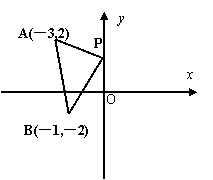
23、点A、B的坐标如图，点P是y轴上一个动点，求PA+PB的最小值。
 |
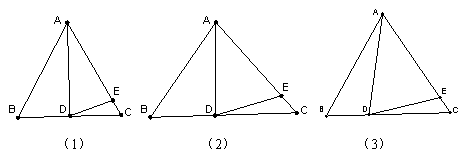
24、（10分）在ΔABC中，AB=AC
（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=__________
（2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=__________
（3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：____________________
（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由。
 |