特殊三角形复习题
一． 精心选一选：（每题3分，共24分。）
1. 等腰三角形的两条边长是4和5，则它的周长是（ ）A12B13C.14 D. 13或14
2. 下列轴对称图形中，对称轴条数最多的是。。。。。。。。。。。。。。。。。。。。（ ）
A．线段 B。角 C。等腰三角形 D。等边三角形
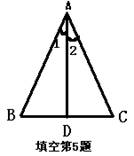
3. 如下图在△ABC中，∠BAC＝90°，AD⊥BC，则图中互为余角的有。。。（ ）
A．2对 B。3对 C。4对 D。5对
4. 在△ABC中，∠C＝40°,∠B=70°,则下面的结论是正确的是。。。（ ）
A．AB＝AC B。AC＝BC C。BC＝AB D。都不相等
5. 以下各组数为连长的三角形中，能组成直角三角形的是（ ）
A．3、4、6 B。15、20、25 C。5、12、15 D。10、16、25
6. 在△ABC中，∠A的相邻外角是110°，要使△ABC为等腰三角形，则底角∠B的度数是（ ）A．70 B。55° C。70°或55° D.60°
7. 下列判断正确的是。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。（ ）
A. 顶角相等的的两个等腰三角形全等
B. 腰相等的两个等腰三角形全等
C. 有一边及一锐角相等的两个直角三角形全等
D. 顶角和底边分别相等的两个等腰三角形全等
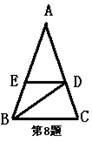
8. 已知，如图在△ABC中，AB＝AC，∠A＝36°，BD是△ABC的角平分线，DE∥BC，则图中等腰三角形的个数是（ ）A．2B。3 C。4 D。5
二． 专心填一填：（每题3分，共30分。）
1. 在△ABC中, ∠ACB＝90°，AB＝10cm,点D为AB的中点，则CD＝_____cm.
2. 在Rt△ABC中, 锐角∠A＝35°，则另一个锐角∠B＝＿＿＿＿＿＿＿。
3. 在△ABC中, ∠A＝120°，∠B＝30°，AB＝4cm,则∠DAC＝＿＿＿＿__。
4. 如图，在△ABC中,AB＝AC，∠1＝∠2，BD＝6cm,则BC＝＿＿＿＿＿。
5. 等腰直角三角形的一条直角边为1cm,则它的斜边上的高线是＿＿＿_cm.
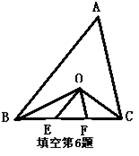
6. 如图,已知在△ABC中,BC＝3，∠ACB和∠ABC的两条角平分线相交于点O，OE∥AB，OF∥AC，则△OEF的周长是＿＿＿＿＿＿＿。
7. 已知等腰三角形一腰上的中线将它周长分成9cm和6cm 两部分，则这个等腰三角形的底边长是＿＿＿8．在Rt△ABC中, AB＝5，BC＝3，则AC＝＿＿＿＿＿＿。
9、如图，有一块直角三角形纸片，两直角边AC＝6厘米，BC＝8厘米，现将直角边AC沿直线折叠，使它落在斜边AB上，且与AE重合，则CD的长为______
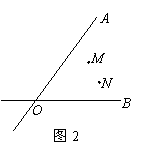
10．如图2，某地有两所大学M、N和两条交叉的公路AO、BO，现计划建一个体育馆，希望体育馆到两所大学的距离相同，到两条公路的距离也相同，则体育馆应建在 .
 | |||
 |
11．如图3，用硬纸片剪一个长为16cm，宽为12cm的长方形，再沿对角线把它分成两个三角形，用这两个三角形可拼出各种三角形和四边形来，其中周长最大的是 cm，周长最小的是 cm.
三． 细心做一做：（每题6分，共36分。）
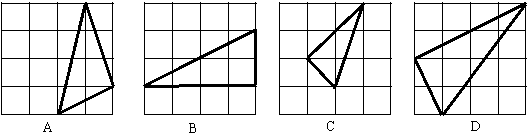
17.如图，在四个均由16 个小正方形组成的网格正方形中，各有一个格点三角形，那么这四个三角形中，与众不同的是 ，不同之处
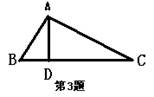
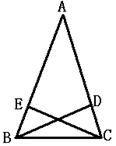3．已知如图，BD、CE是△ABC的高线，且BD＝CE，则△ABC是等腰三角形吗？请你说明理由。
4．如图，在Rt△ABC中, ∠C＝90°，∠A＝30°，
（1）以直角边AC所在的直线为对称轴，将Rt△ABC作轴对称变换，请在原图上作出变换所得的像。
（2）Rt△ABC和它的像组成了什么图形？（＿＿＿＿）（3）利用上面的图形，你能找出直角边BC与
斜边AB的数量关系吗？并请说明理由。
5．已知如图，AD∥BC，∠A＝90°，AD＝BE，，∠EDC＝∠ECD，请你说明下列结论成立的理由：（1）△AED≌△BCE，（2）AB＝AD＋BC。
21．小娇的母亲下岗后，在再就业服务中心的帮助下，开了一家皮衣美容店.一天，一位顾客送来一件皮衣，皮衣上有一个三角形孔洞，让她修补，此时店里有一块颜色、皮质与皮衣完全一样的皮子，其大小与皮衣的孔洞恰好一样，但方向相反，如图7，请你帮小娇的母亲想一想，怎样利用这块皮子（可剪开拼接，损耗不计）补满皮衣上的三角形孔洞.
 |
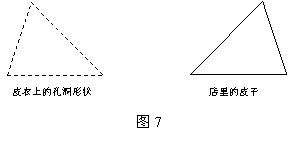23．我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等?
(1)阅读与证明：
对于这两个三角形均为直角三角形，显然它们全等．
对于这两个三角形均为钝角三角形，可证它们全等(证明略)．
对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．
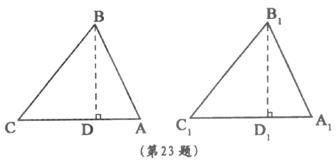求证：△ABC≌△A1B1C1．
(请你将下列证明过程补充完整)
证明：分别过点B，B1作BD⊥CA于D，
B1 D1⊥C1 A1于D1.
则∠BDC=∠B1D1C1=900，
∵BC=B1C1，∠C=∠C1，
∴△BCD≌△B1C1D1，
∴BD=B1D1．
(2)归纳与叙述：
由(1)可得到一个正确结论，请你写出这个结论．
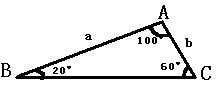
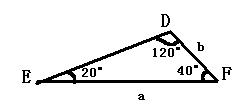6．如图，下面是两张三角形纸片，图1的三角形纸片△ABC的各个角的度数与图2的三角形纸片△DEF的各个角的度数如图所示，且AB＝EF＝a,AC＝DF＝b,将它们剪
成三个等腰三角形，且其中有两组全等的三角形。请在原图上画出剪法，并作必要的说明。