第二章练习卷
一、选择题
1、已知等腰三角形的两边长分别为4、9，则它的周长为（ ）
（A）17 （B）22 （C）17或22 （D）13
2、 等边三角形的对称轴有 （ ）
A 1 条 B 2条 C 3条 D 4条
3、 以下列三个数为边长的三角形能组成直角三角形的是 （ ）
A 1, 1 ,2 B 5, 8 10 C 6 ,7 ,8 D 3 ,4 ,5
4、 三角形内到三角形各边的距离都相等的点必在三角形的 （ ）
A 中线上 B 角平分线上 C 高线上 D 不能确定
5、 下列条件中，不能判定两个直角三角形全等的是 （ ）
A 两个锐角对应相等 B 一条边和一个锐角对应相等
C 两条直角边对应相等 D 一条直角边和一条斜边对应相等
6、等腰三角形的一个顶角为40º，则它的底角为（ ）
（A）100º （B）40º （C）70º （D）70º或40º
7、下列能断定△ABC为等腰三角形的是（ ）
（A）∠A=30º、∠B=60º （B）∠A=50º、∠B=80º
（C）AB=AC=2，BC=4 （D）AB=3、BC=7，周长为13
8、若一个三角形有两条边相等，且有一内角为60º，那么这个三角形一定为（ ）
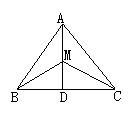
（A）等边三角形 （B）等腰三角形 （C）直角三角形 （D）钝角三角形
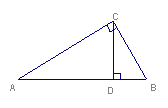
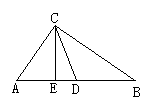
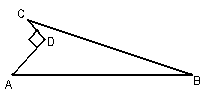
9、如上图∠BCA=90，CD⊥AB，则图中与∠A互余的角有（ ）个
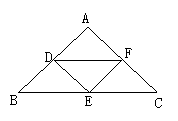
A．1个 B、2个 C、3个 D、4个
10、正三角形ABC所在平面内有一点P，使得⊿PAB、⊿PBC、⊿PCA都是等腰三角形，则这样的P点有（ ）
（A）1个 （B）4个 （C）7个 （D）10个
11.已知∠A=37°，∠B=53°，则△ABC为（ ）
（A）锐角三角形 （B）钝角三角形 （C）直角三角形 （D）以上都有可能
12．下列图形中，不是轴对称图形的是（ ）
（A）线段 （B）角 （C）等腰三角形 （D）直角三角形
13．已知一个三角形的周长为15cm，且其中两边长都等于第三边的2倍，那么这个三角形的最短边为（ ）
（A）1cm （B）2cm （C）3cm （D）4cm
14．具有下列条件的2个三角形，可以证明它们全等的是（ ）
（A）2个角分别相等，且有一边相等;
（B）3个角对应相等;
（C）2边分别相等，且第三边上的中线也相等;
（D）一边相等，且这边上的高也相等
15．在△ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于D，AB=a，则DB等于（ ）
（A）
（B）
（C）
（D）以上结果都不对
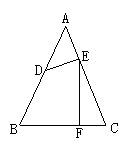
16．如图4所示，△ABC中，AB=AC，过AC上一点作DE⊥AC，EF⊥BC，若∠BDE=140°，则∠DEF=（ ）
（A）55° （B）60° （C）65° （D）70°
(4) (5) (6)
17．一个三角形中，一条边是另一条边的2倍，并且有一角是30°，那么这个三角形是（ ）
（A）直角三角形 （B）钝角三角形
（C）可能是锐角三角形 （D）以上说法都不对
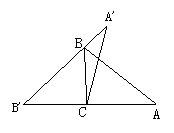
18．如图5所示，在△ABC中，∠A：∠B：∠C=3：5：10，又△A′B′C′≌△ABC，
则∠BCA′：∠BCB′等于（ ）
（A）1：2 （B）1：3 （C）2：3 （D）1：4
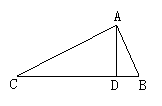
19．如图6所示，△ABC中，∠BAC=90°，AD⊥BC于D，若AB=3，BC=5，则DC的长度是（ ）
（A）
（B）
（C）
（D）
20．如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC2-MB2等于（ ）
（A）9 （B）35 （C）45 （D）无法计算
21. 一架2.5m长的梯子斜靠在一竖直的墙上，这时梯足距墙脚0.7m，那么梯子的顶端距墙脚的距离是 ( )
A. 0.7m B. 0.9m C. 2.4m D. 2.5m
22. 在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，∠C=90°，且c2=2b2，则这个三角形有一个锐角为 ( )
A. 15° B. 30° C. 45° D. 75°
23. 有四个三角形，分别满足下列条件：
(1) 一个内角等于另外两个内角之和；
(2) 三个内角之比为3∶4∶5；
(3) 三边之比为5∶12∶13；
(4) 三边长分别为7、24、25.
其中直角三角形有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
24、下列数组中，是勾股数的是 （ ）
(A)
1，1，
(B) 
(C) 
(D) 
，
，
25、如果把直角三角形的两条直角边同时扩大到原来的2倍，那么斜边扩大到原来的( ).
A.1倍 B. 2倍 C. 3倍 D. 4倍
26、在△ABC中，AB=15,AC=13,高AD=12,则三角形的周长是（ ）
（A）42 (B)32 (C)42或32 (D)37或33.
27、等腰直角三角形的斜边为2，则这个三角形的面积为（ ）
A．2 B。1 C。4
D。
28．△ABC的三边长分别为a，b，c，且a+2ab=c+2bc，则△ABC是（ ）
（A）等边三角形; （B）等腰三角形;（C）直角三角形;（D）等腰直角三角形
29．下列图形中，不是轴对称图形的是（ ）
（A）线段 （B）角 （C）等腰三角形 （D）直角三角形
30．已知等腰△ABC的底边BC=8cm，且│AC-BC│=2cm，那么腰AC的长为（ ）
（A）10cm或6cm （B）10cm （C）6cm （D）8cm或6cm
31．有两个直角三角形，下列条件不能判定它们全等的是（ ）
（A）一锐角和一直角边对应相等 （B）一锐角和斜边对应相等
（C）一边相等，且这边上的高也对应相等（D）斜边和一直角边对应相等
32．在△ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于D，AB=a，则DB等于（ ）
（A）
（B）
（C）
（D）以上结果都不对
33．等腰三角形一腰上的高与另一腰的夹角为40°，则其顶角为（ ）
（A）50° （B）130°
（C）50°或130° （D）55°或130°
34．在一个三角形中，一条边是这条边上中线的2倍，，那么这个三角形是（ ）
（A）直角三角形 （B）钝角三角形
（C）可能是锐角三角形 （D）以上说法都不对
二．填空题
1、一个等腰三角形底上的高、________和顶角的________互相重合。
2、在Rt△ABC中,∠C=90度,∠B=25度,则∠A=______度.
3、 等腰三角形的腰长为10，底边长为12，则其底边上的高为______.
4、已知等边三角形的周长为24cm，则等边三角形的边长为_______cm
5、Rt△ABC的斜边AB的长为10cm，则AB边上的中线长为________
6、在Rt△ABC中，∠C=90º，∠A=30º，BC=2cm，则AB=_____cm。
7、等边三角形两条高线相交所成的钝角为________度
8、若直角三角形的两个锐角之差为24度，则较大的锐角的度数是_________ 。
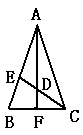
9、如图，在△ABC中，AB=AC，∠BAC与∠ACB的平分线AF、CE相交于点D，且∠B=70º，则∠ADE的度数为_________
10、如图，在Rt
中，CD是AB边上的高，若AC=4，
BC=3 ，则CD=
| ||||||
| ||||||
| ||||||
11．已知等腰三角形一个内角的度数为30°，那么它的底角的度数是_________．
12．等腰三角形的顶角的度数是底角的4倍，则它的顶角是________．
13．等腰三角形的两边长分别为3厘米和6厘米，这个三角形的周长为_________．
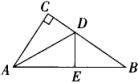
14．如图，在
中，
平分
，则D点到AB的距离为________．
4
5
6
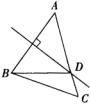
15．如图，在 中， 平分
，若
，则
．
16．如图，
，AB的垂直平分线交AC于D，则
17．如图， 中，DE垂直平分
的周长为13，那么 的周长为__________．
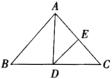
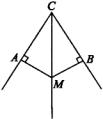
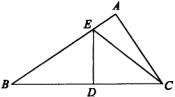
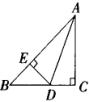
18．如图，如果点M在
的平分线上且
厘米，则
，你的理由是_____________________________________________．
19．如图，已知
边的垂直平分线交
于点
，则
的周长为__________．
20．在△ABC中，到AB、AC距离相等的点在_______上．
21．在Rt△ABC中，∠C=Rt∠，∠A=3∠B+10°，则∠B=_______．
22．△ABC为等腰直角三角形，D、E、F分别为AB、BC、AC边上的中点，则图1中共有_____个等腰直角三角形．
(1) (2) (3)
23．现用火柴棒摆一个直角三角形，两直角边分别用了7根、24根长度相同的火柴棒，则斜边需要用______根．
24．△ABC中，∠ACB=90°，CD⊥AB，垂足是D，E是AB的中点，如果AB=10，BC=5，那么CE=_______，∠A=_____，∠B=______，∠DCE=______，DE=_______．
25．如图2所示，在Rt△ABC中，CD是斜边上的中线，CE是高．已知AB=10cm，DE=2.5cm，则∠BDC=________度，S△BCD=_______cm2．
26．如图3所示，在△ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，则∠DBC=_______．
27．E、F分别是Rt△ABC的斜边AB上的两点，AF=AC，BE=BC，则∠ECF=______．
28．在△ABC中，∠B=2∠C，AD⊥AC，交BC于D，若AB=a，则CD=________．
29、等腰三角形底边长为
，一腰上的中线把其周长分为两部分的差为
.则腰长为
30、如果等腰三角形的顶角等于36°，则底角等于_________度；如果底角等于36°，那么顶角的度数为_________．
31、有一个角等于50°，另一个角等于__________的三角形是等腰三角形．
32、有一个底角为
的等腰三角形的另外两个角的度数分别为________.
33、顶角为 的等腰三角形的另外两个内角的度数分别为_______.
34、有一个内角为
的等腰三角形的另外两个内角的度数为______.
35、有一个内角为
的等腰三角形的另外两个内角的度数为________.
36、如果等腰三角形的三边均为整数且它的周长为
，那么它的三边长为______.
37、在Rt△ABC中，∠C=90°，
①若a=5，b=12，则c=___________；②若a=15，c=25，则b=___________；
③若c=61，b=60，则a=__________；④若a∶b=3∶4，c=10则SRt△ABC=________。
38、直角三角形ABC中的斜边c=10,直角边a=6,则斜边上的中线是____________.
39、现有两根木棒的长度分别是40 cm和50 cm，若要钉成一个三角形木架，其中有一个角为直角，则所需的木棒长度为_____________
40、三角形的三边满足a2=b2+c2,这个三角形是______三角形，它的最大边是_____.
41、已知△ABC中，AB=12，BC=9，那么当AC2=______或______时，△ABC是直角三角形.
42、如果一个直角三角形的三边为三个连续偶数，那么它的三边长为 .
43、等腰三角形的面积为48cm2，底边上的高为6cm，腰长为______.
44、如果
的三边长
满足关系式
，则
=________，
=________，
=________，的形状是______________.
45．等腰三角形的一个外角是100°，则它的底角是_______.
(1) (2) (3)
46．如图（1），L是四边形ABCD的对称轴，如果AD∥BC，有下列结论：（1）AD=AB，（2）AD=CD，（3）AB∥CD，（4）AB⊥BC，其中正确的结论有_____________________．
47．如图(2)所示，AC、BC分别平分∠BAE，∠ABF，如果△ABC的高CD=8cm，那么点C到AE、BF的距离和等于_______．
48．如图(3)在 △ABC中，∠ACB=90°，CE⊥AB，垂足是E，D是AB的中点，如果AB=10，
∠B =30°DE=_______．
49．等边三角形的边长为a，它的面积 ．
50. E. F分别是Rt△ABC的斜边AB上的两点，AF=AC，BE=BC, 则∠ECF=______．
三、解答题
1．如图， 中，
，试说明：
．
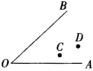
2．如图，求作一点P，使
，并且使点P到
的两边的距离相等，并说明你的理由．
3．如图，已知 中，DE垂直平分AC，交C于点E，交BC于点D，
的周长是20厘米，AC长为8厘米，你能判断出 的周长吗？试试看．
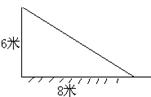
4、 受台风“云娜”影响，一千年古樟在离地面6米处断裂，大树顶部落在离大树底部8米处，损失惨重，问大树折断之前有多高？
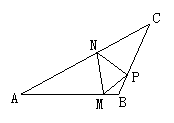
5、如图所示，△ABC中，∠ABC=100°，AM=AN，CN=CP，求∠MNP的度数．
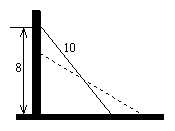
6、如果一个长为10m的梯子，斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，请猜测梯子底端滑动的距离是否会超过1m，并加以说明．
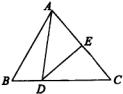
7、如图所示，已知：AB=BC=AC，CD=DE=EC，求证：AD=BE．
8、如图所示，已知：Rt△ABC中，∠C=90°，AC=BC，AD是∠A的平分线．
求证：AC+CD=AB．
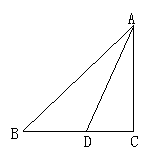
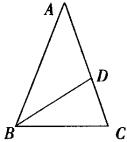9、如图，已知：在
中，
，
，BD是 的角平分线，求
的度数.
10、如图所示的一块地，∠ADC＝90°，AD＝12m，CD＝9m，AB＝39m，BC＝36m，求这块地的面积.
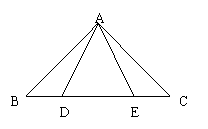
11、如图，已知△ABC中，点D、E在BC上，AB=AC，AD=AE。请说明BD=CE的理由。
 |
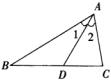
12、如图，已知∠EAC是△ABC的外角，∠1=∠2，AD∥BC，请说明AB=AC的理由。
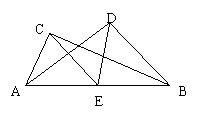
13、如图，△ABC和△ABD中，∠C=∠D=Rt∠，E是BC边上的中线。请你说明CE=DE的理由。
 |
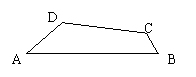
14、如图，在四边形ABCD中，AB=8，BC=1，∠DAB=30°，∠ABC=60°，四边形ABCD的面积为5，求AD的长。
 |