八年级(下)数学同步辅导
第四章 相似图形(§6~§9)
Ⅰ. 梳理知识
1.三角形相似的条件
(1) ，两三角形相似.
(2) ，两三角形相似.
(3) ，两三角形相似.
2.如何寻找和发现相似三角形
两个三角形相似，一般说来必须具备下列六种图形之一：
 |
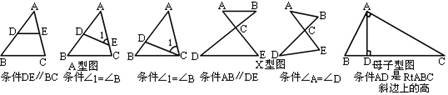只要能在复杂图形中辨认出上述基本图形，并能根据问题需要舔加适当的辅助线，构造出基本图形，从而使问题得以解决.
3.相似三角形与相似多边形的性质
(1)相似三角形的性质
①相似三角形的三边 ，三角 .
②相似三角形的 ， 与 都等于相似比.
③相似三角形周长之比等于 ，相似三角形面积之比等于 .
(2)相似多边形的性质
①相似多边形的对应边 ，对应角 .
②相似多边形的对角线之比、周长之比都等于 .
③相似多边形面积之比等于 .
4.几何变换(按一定的方法把一个图形变成另一个图形)
(1)相似变换：保持图形的形状不变的几何变换叫做相似变换
(2)位似变换
①位似图形：如果两个图形不仅是 图形，而且每组对应点所在的直线都 ，那么这样的两个图形叫做位似图形，这个点叫做 ，这时的相似比又称为 .
②位似图形的性质：位似图形上任意一对对应点到 的距离之比等于位似比.
5.相似三角形的应用——测量旗杆的高度(利用阳光下的影子；利用标杆；利用镜子的反射.)
Ⅱ. 典例剖析
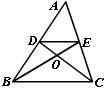
例1.如图，DE∥BC，SΔDOE∶SΔCOB=4∶9，求AD∶BD.
例2.如图，四边形ABCD是平行四边形，AE⊥BC于E，AF⊥CD于F.
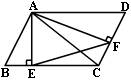(1)ΔABE与ΔADF相似吗？说明理由.
(2)ΔAEF与ΔABC相似吗？说说你的理由.
例3.如图，在RtΔABC中，∠C=90°，AC=4，BC=3.
(1)如图(1)，四边形DEFG为ABC的内接正方形，求正方形的边长.
(2)如图(2)，三角形内有并排的两个相等的正方形，它们组成的矩形内接于ΔABC，求正方形的边长.
(3)如图(3)，三角形内有并排的三个相等的正方形，它们组成的矩形内接于ΔABC，求正方形的边长.
(4) 如图(4)，三角形内有并排的n个相等的正方形，它们组成的矩形内接于ΔABC，请写出正方形的边长.
 |
Ⅲ.同步测试
一、选择题(每小题3分，共30分)
1、在相同时刻的物高与影长成比例，如果高为1.5米的测竿的影长为2.5米，那么影长为30米的旗杆的高是（ ）
A.20米 .B.18米 C.16米 D.15米
2、如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使ΔABE和ΔACD相似的是（ ）
A.∠B=∠C B.∠ADC=∠AEB C.BE=CD，AB=AC D.AD∶AC=AE∶AB
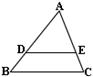
3、如图所示，D、E分别是ΔABC的边AB、AC上的点，DE∥BC，并且AD∶BD=2，那么SΔADE∶S四边形DBCE=（ ）
(A)
(B)
(C)
(D)
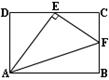
4.在矩形ABCD中，E、F分别是CD、BC上的点，若∠AEF=90°，则一定有（ ）
(A)ΔADE∽ΔAEF (B)ΔECF∽ΔAEF (C)ΔADE∽ΔECF (D)ΔAEF∽ΔABF
 |  |  | |||||
 | |||||||
(第2题图) (第3题图) (第4题图) (第5题图)
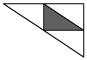
5、厨房角柜的台面是三角形(如图所示)，如果把各边中点连线所围成的三角形铺成黑色大理石(图中阴影部分)，其余部分铺成白色大理石，则黑色大理石面积与白色大理石的面积之比是（ ）
A.1∶2 B.1∶3 C.1∶4 D.1∶5
6、如图，在大小为4×4的正方形网格中，是相似三角形的是（ ）
 |
① ② ③ ④
A.①和② B.②和③ C.①和③ D.②和④
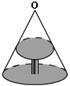
7、如图是圆桌正上方的灯泡O发出的光线照射桌面后，在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m，桌面距离地面1m，若灯泡O距离地面3m，则地面上阴影部分的面积为（ ）
A.0.36πm2 B.0.81πm2 C.2πm2 D.3.24πm2
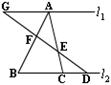
8、如图，直线l1∥l2，AF∶FB=2∶3，BC∶CD=2∶1，则AE∶EC是（ ）
A.5∶2 B.4∶1 C.2∶1 D.3∶2
9、如图，三个正六边形全等，其中成位似图形关系的有（ ）
A.4对 B.1对 C.2对 D.3对
 |  | ||||
 | |||||
(第7题图) (第8题图) (第9题图) (第10题图)
10、平面直角坐标系中，有一条“鱼，它有六个顶点”，则（ ）
A.将各点横坐标乘以2，纵坐标不变，得到的鱼与原来的鱼位似
B.将各点纵坐标乘以2，横坐标不变，得到的鱼与原来的鱼位似
C.将各点横、纵坐标都乘以2，得到的鱼与原来的鱼位似
D.将各点横坐标乘以2，纵坐标乘以
，得到的鱼与原来的鱼位似
二、填空题(每小题4分，共20分)
11、两个相似多边形的一组对应边分别为3cm和4.5cm，如果它们的面积之和为130cm2，那么较小的多边形的面积是 cm2.
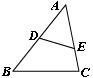12、如图，DE与BC不平行，当
= 时，ΔABC与ΔADE相似.
 | |||||
 | |||||
 | |||||
(第12题图) (第13题图) (第14题图) (第15题图)
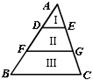
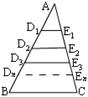
13、如图，AD=DF=FB，DE∥FG∥BC，则SⅠ∶SⅡ∶SⅢ= .
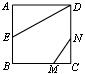
14、如图，正方形ABCD的边长为2，AE=EB，MN=1，线段MN的两端在CB、CD上滑动，当CM= 时，ΔAED与N，M，C为顶点的三角形相似.
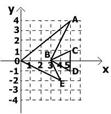
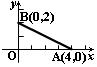
15、如图，在直角坐标系中有两点A(4,0)、B(0,2)，如果点C在x轴上(C与A不重合)，当点C的坐标为 或 时，使得由点B、O、C组成的三角形与ΔAOB相似(至少写出两个满足条件的点的坐标).
三、解答题(每小题8分，共40分)
16、如图，ΔABC中，BC=a.
(1)若AD1=
AB，AE1=AC，则D1E1= ；
(2)若D1D2=D1B，E1E2=E1C，则D2E2= ；
(3)若D2D3=D2B，E2E3=E2C，则D3E3= ；
……
(4)若Dn-1Dn=Dn-1B，En-1En=En-1C，则DnEn= .
17、已知：如图，ΔABC中，∠B=∠C=30°.请你设计三种不同的分法，将ΔABC分割成四个三角形，使得其中两个是全等三角形，而另外两个是相似三角形但不全等的直角三角形.请画出分割线段，标出能够说明分法的所得三角形的顶点和内角度数或记号，并在各种分法的空格线上填空.(画图工具不限，不要求写出画法，不要求说明理由).
 | | |
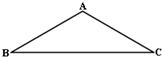分法一 分法二 分法三
分法一：分割后所得的四个三角形中，Δ ≌Δ ，RtΔ ∽RtΔ .
分法二：分割后所得的四个三角形中，Δ ≌Δ ，RtΔ ∽RtΔ .
分法三：分割后所得的四个三角形中，Δ ≌Δ ，RtΔ ∽RtΔ .
18、在比例尺为1∶5000的地图上，一块多边形地区的周长是72cm，面积是320cm2，求这个地区的实际周长和面积.
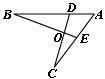
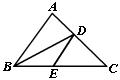19、如图，ΔABC中，BD是角平分线，过D作DE∥AB交BC于点E，AB=5cm，BE=3cm，求EC的长.
20、如图，四边形ABCD、CDEF、EFGH都是正方形.
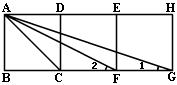(1)⊿ACF与⊿ACG相似吗？说说你的理由.
(2)求∠1+∠2的度数.
五、(本题10分)
21、在ΔABC中，AB=4
如图(1)所示，DE∥BC，DE把ΔABC分成面积相等的两部分，即SⅠ=SⅡ，求AD的长.
如图(2)所示，DE∥FG∥BC，DE、FG把ΔABC分成面积相等的三部分，即SⅠ=SⅡ=SⅢ，求AD的长.
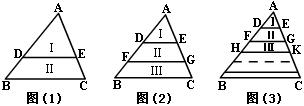如图(3)所示，DE∥FG∥HK∥…∥BC，DE、FG、HK、…把ΔABC分成面积相等的n部分，SⅠ=SⅡ=SⅢ=…，请直接写出AD的长.