八年级数学上学期期中考试试题

八年级数学上学期期中考试试题

（考试时间：120分钟，总分：120分）

题号	一	二	三								得分
			21	22	23	24	25	26	27	28
得分

一.精心选一选：(每小题3分,共30分)

1、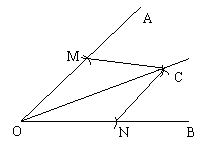课本107页, 画∠AOB的角平分线的方法步骤是：

①以O 为圆心，适当长为半径作弧，交OA于M点，交OB于N点；②分别以M、N为圆心，大于的长为半径作弧,两弧在∠AOB的内部相交于点C；

③过点C作射线OC。 射线OC就是∠AOB的角平分线。请你说明这样作角平分线的根据是（　　 ）

　 A, SSS　　　　　 B, SAS　　　　  C, ASA　　　　　 D, AAS

2、长方形的周长为24cm，其中一边为（其中），面积为，则这样的长方形中与的关系可以写为（　　 ）

　　A.　　B.　　C.　　D.

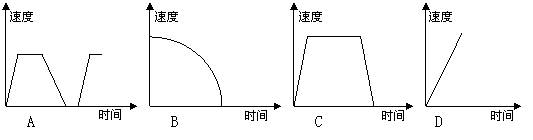
3．小明一出校门先加速行驶，然后匀速行驶一段后，在距家门不远的地方开

始减速，最后停下，下面哪一副图可以近似地刻画出以上情况：(　　)

4. 某班有50人，其中三好学生10人，优秀学生干部5人，在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是 (　 　)
 A．72⁰，36⁰ 　　　 B．100⁰，50⁰　　　 C．120⁰，60⁰　 　 D．80⁰，40⁰

5. 下列条件中，不能判定△ABC≌△A′B′C′的是(　　)

　 A.　　AB=A′B′， ∠A=∠A′， AC=A′C′;

 B.　　AB=A′B′， ∠A=∠A′， ∠B=∠B′

C.　 AB=A′B′，　∠A=∠A′，  ∠C=∠C′;　

D.　 ∠A=∠A′，　∠B=∠B′，　∠C=∠C′

6.已知在一个样本中，50个数据分别落在5个小组内，第一、二、三、五组数据分别为2，8，15，5，则第四小组的频数和频率分别为( 　　　)
　A．25，0.5 　　　B．20，0.5 　 C．20，0.4 　 D．25，0.4

7.要清楚地表明一病人的体温变化情况，应选择的统计图是(　 　 )

A．扇形统计图; B．条形统计图; 　 C．折线统计图; 　 D．以上都不是

8.下列说法中，不能判断两个三角形全等的是（　　　 ）

A.　三条边对应相等的两个三角形全等。　　 

　B.  两条边和一个角对应相等的两个三角形全等。

　C.  两个角和一条边对应相等的两个三角形全等。　

　D.  斜边和一条直角边对应相等的两个直角三角形全等。

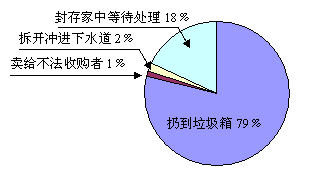9，把过期的药品随意丢弃，会造成

　对土壤和水体的污染，危害人们

　的健康。如何处理过期药品，有

 关机构随机对若干家庭进行调查，

 调查结果如图。其中对过期药品处

 理不正确的家庭达到（　　　　）

　 A， 79﹪　　　　  B，  80﹪

　 C，　18﹪　　　　 D，  82﹪

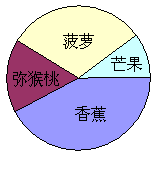
10，两岸关系缓和，今年5·18海交会上，台湾水果成

为一大亮点，右图是其中四种水果成交金额的统计

图，从中可以看出成交金额比菠萝多的水果是（　　）

A，　芒果　　　　  B　　香蕉　　

C　  菠萝　　　　  D　　弥猴桃

二.细心填一题:(每小题3分,共30分)

11．直角三角形两锐角的度数分别为x,y，其关系式为y=90－x，其中变量为　　　　　　 ．

12．函数的自变量x的取值范围是　　　　　　　　 ．

13．若点A（m，2）在函数y=2x－6的图象上，则m的值为　　　　　  ．

14. 在对25个数据进行整理的频数分布表中，各组的频数之和等于______，各组的频率之和等于__________．

15. 函数y=-5x的图象在第　　　　 象限内，y随x的增大而　　　　　  .

16. 已知一次函数y=kx+5的图象经过点（-1，2），则k= 　　　　 .

17．已知：△ABC≌△A′B′C′，∠A=∠A′，∠B=∠B′，∠C=70°，AB=15cm，则∠C′=_________，A′B′=__________．

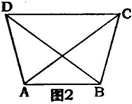
18.如图2，△ABD≌△BAC，若AD=BC，则∠BAD的对应角是________．

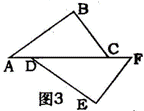19.如图3，在△ABC和△FED，AD=FC，AB=FE，当添加条件__________时，就可得到

△ABC≌△FED．(只需填写一个你认为正确的条件)

20．某水果批发市场香蕉的价格如下表：

购买香蕉数 (千克)	不超过 20千克	20千克以上 但不超过40千克	40千克以上
每千克价格	6元	5元	4元

若小强购买香蕉x千克（x大于40千克）付了y元，则y关于x的函数关系式为 　　　　　　　　　　　　 ．

三.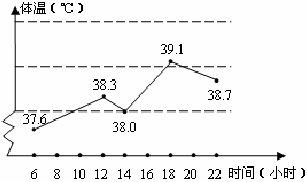解答题:(本大题共60分)

21．(6分)如图，是一位护士统计一位病人的体温变化图：根据统计图回答下列问题：

⑴这天病人的最高体温是　　　

⑵什么时间体温升得最快？
　　　　　　　　　　　

⑶如果你是护士，你想对病人说:____________________　　　　　　 ___　　　　　　　　　　　　 

__________________　　　　　　　　　　　　　　　　　 　　　　　　 .

22．(6分)如图，已知：M是AB的中点，MC=MD，∠1=∠2.

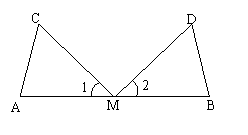求证：AC=BD.

23. (8分)如图，反映了小明从家到超市购物的全过程，时间与距家路程之间关系如图.

（1）　  图中反映了哪两个变量之间的关系？超市离家多远？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

（2）　  小明在超市待了多少时间？小明从超市回到家花了多少时间？

　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

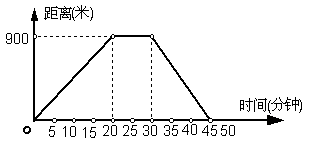（3）小明从家到超市时的平均速度是多少？

　　　　　　　　　　　　　　　　

　　（4）求返回时距离与时间（分）之间的函数关系式。

24.(7分)如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BC=CD，过D作DE∥AB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你作出草图并说明道理.若图是按1︰5000的比例画出, 那么A、B两建筑物之间的距离是多少米？

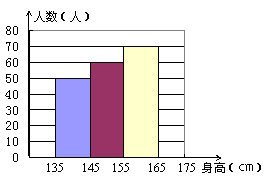25，为了了解我县八年级女生的身高情况，在我校八年级女生中随机抽测了200名女生的身高，统计数据如下：（6分）

组别	身高（㎝）	人数（人）
第一组	135≤X＜145	50
第二组	145≤X＜155	P
第三组	155≤X＜165	70
第四组	165≤X＜175	Q

请你结合所给数据，回答下列问题：

（1）表中的P=　　　 ， Q=　　　 。

（2）请把直方图补充完整。

（3）估计我县八年级女生的身高大约为　　　　㎝

26.(8分)已知:如图,、、、四点在一直线上，，∥，且．

求证：（1）≌；（2）BC∥EF.

27．(9分) 甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题：

(1)　　　　 先出发，先出发　　　　分钟。

　　  　　　　　先到达终点，先到　　　　 分钟。

(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)，在这一时间段内，请你根据下列情形填空：

当　　　　　　　  时，甲在乙的前面时；

当　　　　　　　  时，甲与乙相遇时；

当　　　　　　　  时，甲在乙后面.

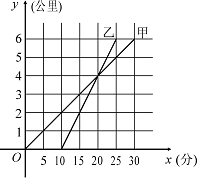(2) 分别求出甲、乙两人的行驶速度；

28，(10分)一次函数y=kx-2的图象经过点A(2，4).

（1）求这个函数的解析式；

（2）请判断点B(-2，-6)是否在这个函数的图象上，并说明理由.

（3）若这个函数与x轴交于C点，与y轴交于D点，求△OCD的面积。

一. 精心选一选

ACCAD　　 CCBDB

二. 细心填一填

（11）,　x, y;　　　　 （12）. x≥3　　　 （13）. m=4　　　　　 （14）.　25,  1;　

（15）.二，四；减小　　　　 （16）.　k=3.　　　 （17）. 70⁰,　 15㎝　

（18）. ∠ABC  或∠CBA　　　（19）. BC=DE,或∠A =∠F或AB∥EF　　

　（20）.　y=4x　(x>40)不写自变量范围不扣分

三. 耐心解一解

21.(1)39.1℃…………………………………2分

(2)14—18时…………………………………2分

(3)您的体温正在下降,请别担心.等,只要符号图形都得分. …………………2分

22.证明:　∵ M是AB的中点

∴　AM=BM　　　……………………2分

在△ACM和△BDM中

　　 AM=BM

∵　 ∠1=∠2

MC=MD

　　　　 ∴　△ACM≌△BDM　　(SAS) ……………………5分

∴　AC=BD　　　　………………………6分

23.(1)距离与时间之间的关系;　　超市离家900米……………………2分

　 (2)小明在超市待了10分钟,　小明从超市回到家花了15分钟 ……………2分

(3)小明从家到超市的平均速度是900÷20=45米/分钟,……………………1分

（4）设函数关系式为y=kx+b　则

解得　 ………………1分

∴　　　 …………………………2分

24. 证明:　∵DE∥AB　　　　　　  (画出图形2分)

∴ ∠A=∠E　　　　……………………1分

在△ABC和△EDC中

　　 ∠A=∠E

∵　 ∠ACB=∠DCE　　

BC=CD

　　　　 ∴　△ABC≌△EDC　　(AAS) ……………………2分

∴　AB=DE　　　　………………………3分

量得　AB=2.5㎝　　……………………1分

　　 2.5:X=1:5000　 解得X=12500厘米=125米

所以, A、B两建筑物之间的实际距离为125米.　 ………………………2分

25.(1)　P=60,　 Q=20　 ………………2分

(2) 略……………………2分

(3) 153㎝　 ………………………2分

26 证明:　∵　AB∥DE　　　　　　 

∴　∠A=∠D　　　　……………………1分

　 ∵　AF=CD

∴　AF+FC=CD+FC

 即　AC=DF…………………………3分

在△ABC和△DEF中

　　　 AB=DE

∵　 ∠A=∠D　

AC=DF

　　　　 ∴  △ABC≌△DEF　　(SAS) ……………………6分

∴ ∠ACB=∠DFE　　　 ………………………7分

∴　BC∥EF　　　…………………………8分

27　 (1)　甲 ；　10分钟； 乙；　5分钟.　…………………………………4分

 (2) x＜20　　 x=20　　 x＞20　　…………………………3分

(3) 根据图象用路程除以时间即得: 甲的速度为每分钟0.2公里，

乙的速度为每分钟0.4公里 .　　………2分

28，（1）∵  y=kx-2经过A(2,4)

　　　　∴　4=2k-2　 解得: k=3　 …………………………2分

　　　　∴　y=3x-2　　　　　　　  …………………………3分

(2) ∵ 当x=-2时　y=3×(-2)-2 = -8 ≠ -6　　…………………2分

　　∴　点B(-2,-6)不在函数的图象上.　 …………………………3分

(3) 令y=0　 则0=3x-2　　　解得  x=　  

　　∴C(　　 ,0)  即 OC=　　 …………………………1分

 令x=0　 则y=-2　　　

　　∴　D(0, -2)　　即　OD=2　　…………………………2分

∴　　　　　　　　　　　　　　　　　　　 …………………4分