八年级数学第一学期期中调研卷
一、选择题（每题2分，共20分）
1．4的算术平方根是( )
A．±2 B．2 C．－2 D．8
2. 下列长度的三条线段，能组成直角三角形的是( )
A．1cm、2cm、3cm B．3cm、3cm、4cm
C．5cm、4cm、3cm D．6cm、3cm、4cm
3.若等腰三角形两边长分别为3和4，则它的周长是 ( )
A．8 B．10 C．11 D．10或11
4．估计
的大小应该是
( )
（A）在6～7之间 （B）在7～8之间
（C）在8～9之间 （D）在9～10之间
5. 如图，
的周长是28 cm，△ABC的周长是22 cm，
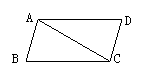则AC的长为（ ）
A．6 cm B．12 cm
C．4 cm D．8 cm
6. ．下列图形中，中心对称图形是（ ）
 |
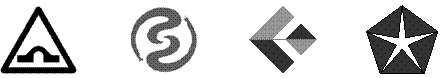（A） （B） （C） （D）
7. 把一正方形纸片按图中（1）、（2）的方式依次对折后，再沿（3）中的虚线裁剪，最后把（4）中的纸片打开铺平，所得图案应该是下面图案中的（ ）
 |
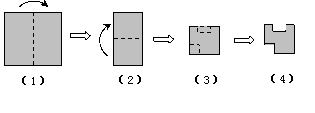
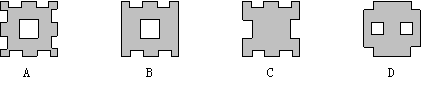8.下列命题中，错误的是（ ）。
A、等边三角形的三条边相等
B、平行四边形的对角线互相平分且相等
C.等腰梯形的两条对角线相等
D、等腰三角形底边上的中点到两腰的距离相等
9．
如图，在长方形ABCD中，对角线AC、BD相交于点O，若OA＝2，则BD的长为（ ）
A、4 B、3 C、2 D、1
10．把n个边长都为lcm的正方形按如图所示的方法摆放，点A1，A2，……，An分别是正方形的中心，则n个这样的正方形重叠部分的面积和为( )
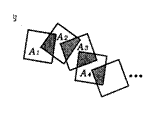A．
cm。 B．
cm2
Ｃ．
cm2 D．
cm2
二、填空题（每空2分，共20分）
11．一个正方体纸盒，它的容积为0.064m
，正方体纸盒的棱长是_________.
12． 
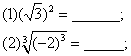(3)
13．某零件的长度是1.30cm，这个数据有 个有效数字．
14．若
+a=0，则a＝_______________．
15如图，在△ABC 中，AD⊥BC于D.请你再添加一个条件，就可
以确定△ABC 是等腰三角形.你添加的条件是 .
 |
16．如图，□ ABCD的对角线相交于点O，图中全等三角形有_________对
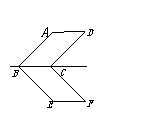17．如图，若□ABCD与□EBFC关于BC所在直线对称，∠ABE＝90°，
则∠F ＝ °．
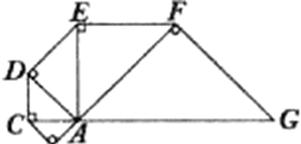
18. 如图,直角三角形ABC是直角边长为1的等腰直角三角形，以直角三角形ABC的斜边AC为直角边，画第二个等腰直角三角形ACD，再以直角三角形ACD的斜边AD为直角边，画第三个等腰直角三角形ADE，…，依此类推，第5个等腰直角三角形AFG的斜边AG长是____.
 |
三、求下列各式中的x（每题4分，共8分）
19．
．
20. 
.
四、计算与说理（每题5分，共20分）
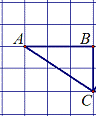
21． 如图，某人要横渡一条河，由点A游到点B,由于水流的影响，实际上岸地点C偏离点B 300m，结果他在水中实际游了500m，求该河流的宽度.
 |
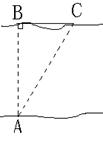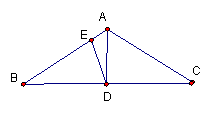
22. 如图，△ABC中，AB=AC，∠BAC=120°，AD是BC
边上的中线，且BD=BE，计算∠ADE的度数。
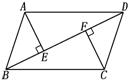
23．如图，在
中，BD是对角线，
，垂足分别为
，
． 说明
．
.
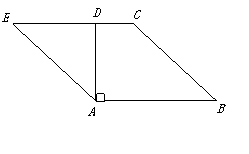
24．如图，在梯形
中，
，延长
到点，使
，连接
．
（1）说明
；
（2）若
，求四边形
的面积.
五、操作与解释 （每题6分，共18分）
25．(1） 请画出下面这个轴对称图形
的对称轴.
（2）如图，在方格纸中画出△ABC绕点C顺时针方向旋转900后得到的△CDE．
26. 近年来，国家实施农村医疗卫生改革，某县计划在甲村、乙村之间设一座定点医疗站点P，甲、乙两村座落在两相交公路内(如图所示)。医疗站必须适合下列条件：①使其到两公路距离相等，②到甲、乙两村的距离也相等，请你经过画图确定P点的位置。
|
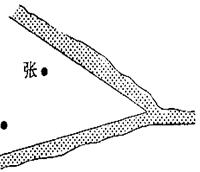
乙
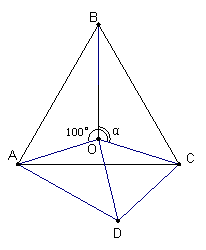
27. 如图，点O是等边三角形ABC内一点，∠AOB＝100°，∠BOC＝α．把△BOC绕点C按逆时针方向旋转60°得△ADC，连接OD．
(1)说明△COD是等边三角形；
(2)填空：用α表示∠AOD的结果为 ；用α表示∠ADO的结果为 ．
 |
六、探索与思考（第28题6分，第29题8分，共14分）
28．如图，四边形ABCD中，AD不平行BC，现给出三个条件：①∠CAB=∠DBA，②AC=BD，③AD=BC.请你从上述三个条件中选择两个条件，使得加上这两个条件后能够推出四边形ABCD是等腰梯形，并加以说明（只需说明一种情况）.
29．把平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′ 处，折痕为EF．
（1）说明△ABE≌△AD′F；
（2）连接CF，四边形AECF的四条边相等吗？为什么？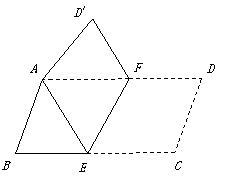 
参考答案及评分标准
一、选择题（每题2分，共20分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | D | D | D | B | B | B | A | C |
二、填空题（每空2分，共20分）
11．0.4m 12．3,-2,>
13．三 14． 
15．BD=CD 16．4 17．
450 18． 
三、求下列各式中的x（每题4分，共8分）
19．解： 
……………………………2分
∴x＝
3．…………………………4分
20．解：x-1=-3，……………………………2分 ，
即x＝-2．…………………………… …4分
四、计算与说理（每题5分，共20分）
21．解：AB=
(m)
…………………………………………….4分
答：河流的宽度为400m……………………5分
22．解：∵AB=AC，∠BAC=120°，AD是BC边上的中线,
∴∠B=∠C=300
………………………………………………………………………2分
又∠BDE=
………………………………………………………3分
∴∠ADE=150……………………………………………………….5分
23．解：说明△AEB≌△DEC,…………………4分
得AE=CF……………………………..5分
24．解：(1)由∠E=∠B=450
得∠E+∠C=1800
∴………………………………………………………………3分
(2)
四边形的面积=3×(3-1)=6…………………………………5分
五、操作与解释 （每题6分，共18分）
25．解：图:略………………………每小题画图正确得3分,共6分.
26．解：:略………………………………………画图正确得6分
27. 解：(1)因为△ADC是由△BOC旋转60°后得到的，所以△ADC≌△BOC，∠OCD＝60°．
因为△ADC≌△BOC，所以CO＝CD．所以∠ODC＝∠DOC＝60°．所以△COD是等边三角形．…………………………………………………………………………4分
(2)因为∠DOC＝60°，所以∠AOD＝360°－100°―α―60°＝200°―α．
…………………………………………………………………………………5分
因为△ADC是由△BOC旋转后得到的，所以△ADC≌△BOC．
所以∠ADC＝∠BOC＝α，所以∠ADO＝α－60°…………………………………6分
七、探索与思考（第28题6分，第29题8分，共14分）
28． 解：选择②③两个条件, ∵∴AC=BD，AD=BC.又DC=DC,
∴△ADC≌△DBC,
∴∠ADC=∠DBC, ∠DAC=∠CBD, AD=BC, ∴△AOD≌△BOC,则OA=OB.
………………………………………………………………………3分
∴∠OAB=∠OBA, ∴∠DAB=∠CBA,∴∠ADC+∠DAB=
,∴CD∥AB,
又AD=BC,
则四边形ABCD是等腰梯形……………………………………………6分
29．解：(1)∵∠
AF=∠BAE, ∠AF=∠ABE,A=AB ……2分
∴ △ABE≌△AD′F…………………………………………4分
(2) 四条边相等…………………………………………5分
由(1)得△ABE≌△AD′F, ∴FA=AE,又AE=EC,则FA=EC,又FA∥EC , ∴四边形AECF是平行四边形,………………………………7分
∴AE=FC,又∵FA=AE, ∴ FC=FA
∴ AE=EC=FC=FA………………………………………………8分