八年级数学第一学期期中练习卷(一)
一、选择题(每小题2分，共20分)
1．2的算术平方根是 （ ▲ ）
（A）－ （B） （C）± （D）4
2．近似数2.023的有效数字是 （▲ ）．
（A）1个 （B）2个 （C）3个 （D）4个
3.下列图形中，轴对称图形的是（ ）
4． 下列各数组中，不是勾股数的是 （ ▲ ）．
（A）5，12，13 （B）7，24，25
（C）8，12，15 （D）3k，4k，5k（k为正整数）
5． 在4，3.5，π，,，五个数中，无理数有 （▲ ）．
（A）1个 （B）2个 （C）3个 （D）4个
6．某数的平方根等于它的立方根，则这个数是 （ ▲ ）．
（A）1 （B）－1 （C）0 （D）以上都不对
7． 下列条件中，能说明四边形ABCD是平行四边形的是 （ ▲ ）．
（A）∠A＝30°，∠B＝150°，∠C＝30°，∠D＝150°
（B）∠A＝60°，∠B＝60°，∠C＝120°，∠D＝120°
（C）∠A＝60°，∠B＝90°，∠C＝60°，∠D＝150°
（D）∠A＝60°，∠B＝70°，∠C＝110°，∠D＝120°
8． 下列说法中，正确的是 （▲ ）．
（A）在成中心对称的图形中，连结对称点的线段不一定都经过对称中心
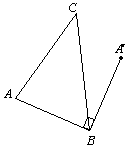
（B）在成中心对称的图形中，连结对称点的线段都被对称中心平分
（C）若两个图形的对应点连成的线段都经过某一点．那么这两个图形一定关于这一点成中心对称
（D）以上说法都正确
9．
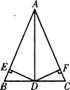如图，△ABC中AB = AC，AD是角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F.下列结论中,不正确的是 (▲ )
（A）DA平分∠ EDF （B）AD上的点到AB、AC 的距离相等
（C）AE = AF （D）AB、AC上的点到AD的距离相等
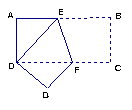10、长方形ABCD中，AD=4cm，AB=10cm，按下图方式折叠，使点B与点D重合，折痕是EF，则DE等于 （ ▲ ）
A、4.2cm B、5.8cm
C、4.2cm或5.8cm D、6cm
二、填空题（每题3分，共18分）
11．在△ABC中，∠A＝60°，∠B＝ ▲ 时，△ABC是等边三角形．
12.计算: ( )3= ▲ ．
13.比较大小: 2 ▲ 3.
14．如图，在△ABC 中，∠BAD＝∠CAD.请你再添加一个条件，就可
以确定△ABC 是等腰三角形.你添加的条件是 ▲ .
 |
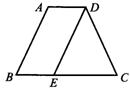15．如图，等腰梯形ABCD中，AD∥BC，AD＝3，AB＝6，BC＝8.
若DE∥AB，则△DEC的周长是 ▲ ．
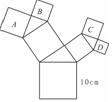16．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为10cm，正方形A的边长为6cm、B的边长为5cm、C的边长为5cm，则正方形D的边长为 ▲ 。
三. 解答题（每题4分，共12分）
17.在数轴上作出表示 - 的点.
18.求 49x2 = 25中的x.
19.求(x+3)3 = - 64中的x.
四、（每题5分，共10分）
20. 在5×7的方格纸上，任意选出5个小方块，
涂上颜色，使着色图形为轴对称图形，并画
出其对称轴（要求：着色出一个图形，并画
出一条对称轴即可）．
 |
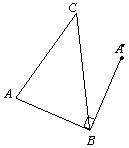
21.△ABC的边AB绕点B旋转到图中BA′的位置，点A′是A
的对应点，画出△ABC绕点B旋转后的图形．
五、（每题5分，共15分）
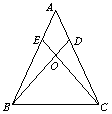
22.如图，在△ABC中，AB＝AC，∠ABD＝∠ACE， BD，CE
相交于点O，猜想：BO＝CO成立吗？并说明理由．
23．如图，已知
是∠BAC的角平分线，
，
，垂足分别是
、
。请你说明垂直平分
。
 |
24．如图，在
中，点
分别是
边的中点，
若把
绕着点顺时针旋转
得到
．
（1）请指出图中哪些线段与线段
相等；
（2）试判断四边形
是怎样的四边形？说明你的结论．
六、（每题6分，共12分）
25．现有一块等腰直角三角形木板，你能通过剪切，
使它成为一个含有45°角的平行四边形吗？
请你设计一个最简的方案，并说明你的方案的正确性．
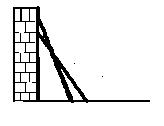26、消防队有一架云梯长25米（如图），将它斜靠小明家所在住宅楼的在一面墙上，当梯子底端离墙7米时，顶端恰好落在小明家的窗台上.
（1）小明家的窗台距地面有多高？
（2）小颖家住在小明家的正楼下，两家窗台相距4米，小明认为，只要将梯子的底部沿水平方向向外拉动了4米？其顶端一定会落在小颖家的窗台上，小明的话对吗？为什么？
七.(本题6分)
27.先观察下列等式，再回答问题：
①
②
③
（1）根据上面三个等式提供的信息，请猜想
的结果，并进行验证；
（2）请按照上面各等式反映的规律，试写出用
（为正整数）表示的等式。
八、（本题7分）
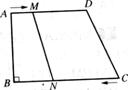28．如图，在梯形ABCD中，AD∥BC，∠B = 90°，AB=14cm，AD=15cm，BC=21cm，点M从A点开始，沿AD边向D运动，速度为1厘米/秒；N从C开始，沿CB边向点B运动，速度为2米/秒. 点M、N分别从A、C出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒.
(1)当t为何值时,四边形MNCD是平行四边形?
(2) 当t为何值时,四边形MNCD是等腰梯形?
答卷纸
| 小 计 | 总分 | ||||||||
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | |
| 得 分 | |||||||||
注意事项：
1．答题前务必将密封线内的项目填写清楚。
2．用钢笔或圆珠笔（蓝色或黑色）在答卷纸上书写，字体工整、笔迹清楚。在草稿纸、试卷上答题无效。
一、选择题（每小题2分，共20分）
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（每小题3分，共18分）
11． ．
12． ．
13． ．
14． ．
15． ．
16． ．
三、（每小题4分，共12分）
17.
18.
19.
四、（每小题5分，共10分）
20.
|
21. 
五、（每题5分，共15分）
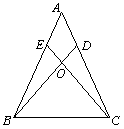22.
23．
 |
24．（1）
（2）
六、（每题6分，共12分）
25． 
26．（1）
（2）
七.(本题6分)
27．（1）
（2）
八、（本题7分）
28．
参考答案及评分标准
一、选择题(每小题2分，共20分)
1.B 2.D 3.D 4.C 5.B 6.A 7.A 8.B 9.D 10.A.
二、填空题（每题3分，共18分）
11. 60° 12..－ . 13.＜. 14. 略 . 15. 17 16. .
三. 解答题（每题4分，共12分）
17.数轴画对且表示-正确…3′,指出结果…4′
18.解 x2 = ,…2′ x = ±. …4′
19.x+3 = ,…2′ x = -7. …4′
四、（每题5分，共分）
20,21题略
五、（每题5分，共15分）
22.成立……….1分,说理由正确 ……….5分
23. 略
24．解：（1）
······················································ 1分
···································································· 2分
（2）四边形是平行四边形······································· 3分
说明：绕点顺时针旋转
，得到
又
是
的中点，
四边形是平行四边形．··········································································· 5分
六.(每题6分,共12分)
25．作等腰直角三角形底边上的中线CD，交AB于点D，将等腰
△ABC分成两个全等的等腰直角三角形，如图翻折其中一个三角形使得DC与CD重叠就可得到一个含有45°角的平行四边形．········ 2分
因为CD是等腰△ABC底边上的中线，
所以AD＝BD，即AD＝CB′．
又因为△ABC是等腰三角形
所以∠A＝45°，AC＝CB，即AC＝DB′．
所以四边形ACB′D，是一个含有45°角的平行四边形．
理由是：有两组对边相等的四边形是平行四边形．················································· 6分
26. (1)24米；…3′（2）不对，＞20.…6′
七、（本题6分）
27. （1）.....2分，验证…….3分（2）…….6分.
八、（本题7分）
28.（1）15-t=2t，t=5，即当t=5时，四边形MNCD是平行四边形；…3′
（2）作ME⊥BC，DF⊥BC，垂足分别是E、F，由于MN = DC ，所以NE = CF，于是有：2t-（15-t）=12，t=9, 即当t=9时, 四边形MNCD是等腰梯形… 7′