八年级数学第一学期期中练习卷(二)
(时间100分钟 满分100分)
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 总 分 |
| 得 分 |
|
|
|
一、选择(每小题2分，共16分)
1．4的平方根是 ( )．
A．± 4 B．4 C．± 2 D．2
2．－8的立方根是 ( )．
A．－2 B．2 C．±2 D．不存在
3．实数，π，，，－中，有理数有 ( )．
A．1个 B．2 个 C．3个 D．4个
4．下列图形中，轴对称图形是 ( )．
 |
A． B． C． D．
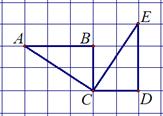5．如图，△ABC旋转后得到△EDC．
其中，点A旋转后的对应点是 ( )．
A． 点B B． 点C
C． 点D D． 点E
(第5题图)
6．在下列四组数中，不是勾股数的一组数是 ( )．
A．a=15，b=8，c=17 B．a=9，b=12，c=15
C．a=3，b=5，c=7 D．a=7，b=24，c=25
7．等腰三角形的一个内角为80°，则其底角的大小为 ( )．
A．50° B．80° C．50°或80° D．100°
8．已知下列说法：
①平行四边形的对角线互相平分；②对角线互相平分的四边形是平行四边形；
③等腰梯形的对角线相等； ④对角线相等的四边形是等腰梯形．
其中，正确的说法有 ( )．
A．1个 B．2 个 C．3个 D．4个
二、填空(每空2分，共20分)
9． 的相反数是 ．
10．用“＜”或“＞”填空： + 1 4．
11．如果实数x满足4x2＝25，那么x的值为 ．
12．据江苏省统计局反馈，南京市2006年实现GDP产值277 400 000 000元．用科学计数法表示这一近似数的结果为 元(保留3个有效数字)．
13．如果正方形面积为20，那么比它的边长小的最大正整数是 ．
14．如图，如果使一个正六边形旋转后与原来的图形重合，那么旋转角最小是 °．
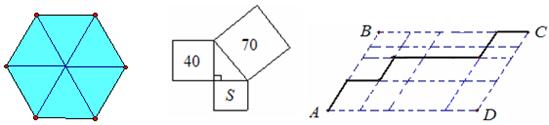
(第14题图) (第15题图) (第16题图)
15．如图，图中的字母S所代表的正方形的面积为
16． 如图，四边形ABCD中，所有的横向线段均相互平行，其余的所有线段也都相互平行．如果AB+BC＝7，那么，图中折线(由所有的粗黑线段构成)的长为 ．
17．如图，△ABC中，∠BAC＝90°，点D为边BC的中点．如果∠B＝70°，
那么∠ADB＝ °．
 |
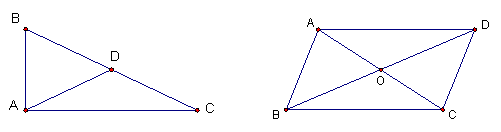(第17题图) (第18题图)
18．如图四边形ABCD中，AB＝CD，AC交BD于点O．如果想使该四边形成为平行四边形，那么只需添加条件： ．
三、计算 (每题5分，共20分)
19．求满足式子(x－1)3＝－27的x的值．
20．如下图，在△ABC中，边AB的垂直平分线交BC于点D．如果AC+BC＝7，
求△ADC的周长．
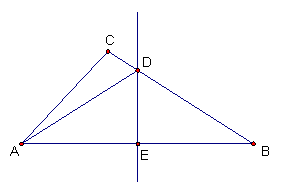
21．如图，△ABC中，AB＝AC， 点D为边BC的中点，∠BAC＝110°，求∠B和∠BAD的大小．
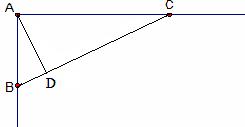
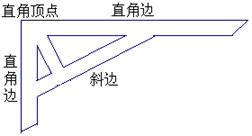
22．木工师傅为了让直尺经久耐用，常常在直尺的直角顶点与斜边之间加一个小木条，如下左图所示．下右图为其示意图．若∠BAC＝90°，线段AB的长为5，线段AC的长为12，试求出小木条AD的最短长度．
四、作图(每题5分，共15分)
23．利用网格线，分别作出三角形关于直线l和点O的对称图形．
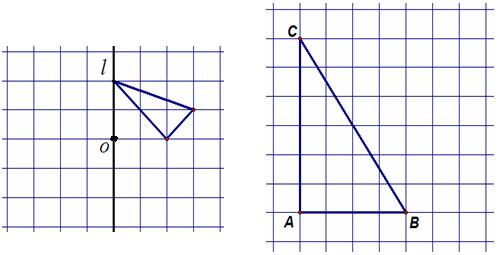
(第23题图) (第24题图)
24．利用网格线作图：在BC上找一点P，使点P到AB和AC的距离相等．然后，在射线AP上找一点Q，使QB＝QC．
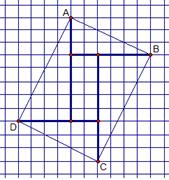
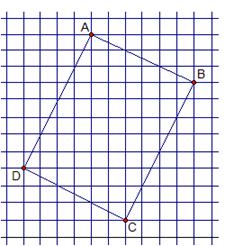25．如下图，小方格的面积都为1．四边形ABCD的顶点都在格点上，求该四边形的面积．
五、说理(第25题5分，第26题8分，共13分)
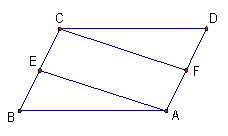26．如下图，在□ABCD中，点E、F分别为边BC、AD的中点，连AE、CF．问：四边形AECF为平行四边形吗？为什么？
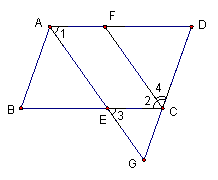
27．如下图，在□ABCD中，∠BAD、∠BCD的平分线分别交BC、AD于点E、F，AE、DC的延长线交于点G．试说明四边形AFCG为等腰梯形．
六、探究(第28题9分，第29题7分，共16分)
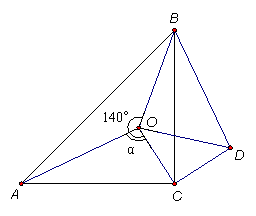
28．如图，点O是等腰直角三角形ABC内一点，∠ACB＝90°，∠AOB＝140°，∠AOC＝α．将△AOC绕直角顶点C按顺时针方向旋转90°得△BDC，连接OD．
(1)试说明△COD是等腰直角三角形；
(2)当α＝95°时，试判断△BOD的形状，并说明理由．
 |
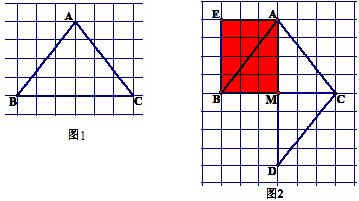
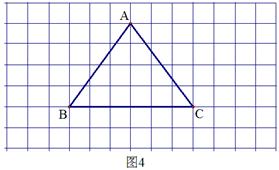
29．把三角形形状的纸片放在方格纸上，使其每一个顶点都在格点上，如图1所示(方格边长均为1)．对这个三角形进行剪切、拼接后，可以得到一个平行四边形，如图2中阴影部分所示．
剪切、拼接的方案如下：如图2，取BC的中点M，连AM．剪下△AMC后，沿直线BC翻折，所得图形称为三角形DMC；再把三角形DMC沿射线CA方向平移线段CA的长度后，可得到平行四边形AEBM．
我们约定：剪切、拼接时，纸片的每一部分都要被用到，而且不得用所给纸片以外的纸片．
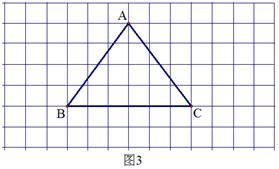(1)请你采用不同的剪切、拼接方案，也得到一个平行四边形，并说明你的剪切、拼接方案，同时在图3中用阴影表示出你得到的平行四边形；
(2) 对这个三角形进行剪切、拼接后，也可以得到一个梯形。试在图4中，用阴影表示出你得到的梯形(不必说明剪切、拼接方案，但须保留作图痕迹)．
参考答案和评分标准
一、选择题(每小题2分，共16分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | A | B | A | D | C | C | C |
二、填空题(每空2分，共20分)
9．－ 10．＜ 11．± 12．2．77×1011 13．4
14．60 15．30 16．7 17．40 18．AD＝BC，AB∥CD等．
19．因为(x－1)3＝－27，所以x－1是－27的立方根，所以x－1＝．…………3分
所以x－1＝－3，得x＝－2． …………5分
20．因为点D在边AB的垂直平分线上，所以DA＝DB． …………2分
所以CD+ DA＝CD+ DB＝CB． …………4分
所以△ADC的周长＝AC+CD+ DA＝AC+BC＝7． …………5分
21．因为AB＝AC， 点D为边BC的中点，所以AD是∠BAC的平分线，且AD ⊥BC．
…………2分
因为∠BAC＝110°，所以∠BAD＝55°． …………4分
所以∠B＝35°． …………5分
22．当AD⊥BC时，小木条AD的长度最短． …………1分
此时，因为∠BAC＝90°，AB＝5，AC＝12，所以BC＝13． …………3分
因为三角形ABC的面积＝AB×AC＝BC×AD，所以AD＝ ． …………4分
答：小木条AD的最短长度为． …………5分
23．做对一个图得3分，做对两个图得5分．图略．
24．做对一个图得3分，做对两个图得5分．图略．
25．
如图，分割四边形ABCD正确．…………2分
四边形的面积＝×6×3×2+×4×8×2+2×5
＝60． ……………5分
(猜想四边形ABCD为长方形而未说明，但计算结果
正确，得2分)
26．由平行四边形性质可知，CE∥FA， BC＝AD． …………2分
因为点E、F分别为边BC、AD的中点，所以CE＝BC，FA＝AD．
所以CE＝FA． …………4分
又因为CE∥FA，所以四边形AECF为平行四边形． …………5分
27．因为AE、CF分别为∠BAD、∠BCD的平分线，
所以∠1＝∠BAD，∠2＝∠4＝∠BCD． …………1分
由平行四边形性质可知，∠BAD＝∠BCD． …………2分
所以∠1＝∠2＝∠4． …………3分
由AD∥BC可得∠1＝∠3．又因为∠1＝∠2，所以∠2＝∠3．所以AG∥FC．
因为AG≠FC．所以四边形AFCG为梯形． …………5分
因为AG∥FC，所以∠4＝∠G．又因为∠1＝∠4，所以∠1＝∠G．
又因为四边形AFCG为梯形，所以四边形AFCG为等腰梯形． ……………8分
28．(1)因为△BDC是由△AOC旋转90°后得到的，所以△BDC≌△AOC，∠OCD＝90°．
………… 2分
因为△BDC≌△AOC，所以CD＝CO． ………… 4分
又因为∠OCD＝90°，所以△COD是等腰直角三角形． ………… 5分
(2)△BOD为等腰三角形． ………… 6分
当α＝95°时，因为∠DOC＝45°，所以∠BOD＝360°－140°―95°―45°＝80°．
因为△BDC≌△AOC，所以∠BDC＝∠AOC＝95°，所以∠BDO＝95°－45°＝50°．
………… 8分
又因为∠BOD＝80°，所以∠OBD＝50°．
所以∠BDO＝∠OBD．所以△BOD为等腰三角形． ………… 9分
29．(1) 平行四边形FECB为所求(如图3)．(答案不唯一，如图3另解等)
………… 2分
剪切、拼接的方案：如图3，取BC的中点D，取AC的中点E，连DE．剪下△ADE后，使其绕点D旋转180°，所得图形称为△BDF．此时，可得到平行四边形FECB． ………… 4分
 |
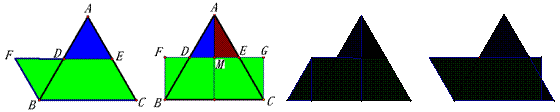(图3) (图3) 另解 (图4) (图4)另解
(2) 如图4(绿色部分)(答案不唯一，如图4另解等) ………… 7分