八年级数学上期末复习卷
班级 座号 姓名 成绩
一、填空:(每小题2分,共24分)
1.单项式![]() 的系数是
,次数是
.
的系数是
,次数是
.
2.若函数![]() ,当
,当![]() =2时,
=2时,![]() =3,则当
=3,则当![]() =-2时,
=-2时,![]() =
.
=
.
3.(-3,2)与点Q关于原点对称,则点Q在第 象限.
4.请写出一个图象经过点(1,4)的函数解析式: .
5.因式分解:![]() =
.
=
.
6.某班50名学生在数学测试中,分数段在90~100分的频率为0.1,则该班在这个分数段的学生有 人.
7.在△ABC中,边AB、AC的垂直平分线相交于P点,则线段PA、PB、PC的大小关系是 .
|
9.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分
线交BC于点D,交AB于点E,DB=10,则AC= .



 10.下面四个图形中,从几何图形的性质考虑,哪一个与其它三个不同?请指出这个图形,并简述你的理由.答:图形
;理由是
.
10.下面四个图形中,从几何图形的性质考虑,哪一个与其它三个不同?请指出这个图形,并简述你的理由.答:图形
;理由是
.
11.方程组![]() 的解是一次函 数
与一次函数
图象的交点坐标,该坐标为
.
的解是一次函 数
与一次函数
图象的交点坐标,该坐标为
.
12.多项式![]() 加上一个单项式后,使它能成为一个整式的完全平方,则加上的单项式可以是
.(要求写三个)
加上一个单项式后,使它能成为一个整式的完全平方,则加上的单项式可以是
.(要求写三个)
二、选择:(每小题2分,共16分)
13.下列运算中,正确的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14.下面运算正确的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
15.如图是某个地区居民文化程度统计图,下列说法错误的是( ).
|
B.本科文化程度的人最少
C.表示“专科”扇形的圆心角为19°
D.高中文化程度的人数占总数的30%
16.小亮在镜中看到身后墙上的时钟如图,你认为实际时间最接近八点的是( ).
|
A B C D
A B C D
17.函数![]() 随自变量
随自变量![]() 的增大而增大,图象与
的增大而增大,图象与![]() 轴交于(-4,0),则
轴交于(-4,0),则
![]() >0时,
>0时,![]() 的取值范围是( ).
的取值范围是( ).
A.![]() >-4 B.
>-4 B.![]() >0 C.
>0 C.![]() <-4 D.
<-4 D.![]() <0
<0
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
19.在直角坐标系中,O为坐标原点,已知点A(1,1),在![]() 轴上确定 点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( ).
轴上确定 点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( ).
A.1个 B.2个 C.3个 D.4个
20.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:![]() ,因此,4,12,20都是“神秘数”.以下四个数中“神秘数”是( ).
,因此,4,12,20都是“神秘数”.以下四个数中“神秘数”是( ).
A.2006 B.2008 C.2010 D.2012
三、计算:(每小题4分,共8分)
21.因式分解:![]() ; 22.计算:
; 22.计算:![]() .
.
四、(每小题5分,共10分)
23.先化简,再求值:![]() ,其中
,其中![]() ,
,![]() .
.
24.阅读下列因式分解的过程,再回答所提出的问题:
![]()
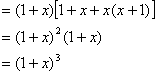
(1)上述分解因式的方法是 ,共应用了 次;
(2)若分解![]() ,则需应用上述方法
次,
,则需应用上述方法
次,
结果是 ;
(3)分解因式![]() (n为正整数)=
.
(n为正整数)=
.
五、(每小题6分,共24分)
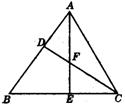
25.如图,在△ABC中,点D在AB上,点E在BC上,BD=BE.
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明.
你添加的条件是: .
(2)根据你添加的条件,再写出图中的一对全等三角形 .(只要求写出一对全等三角形,不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)
26.下图是根据某市2006年12月1日至6日最高气温所绘制的条形统计图.
(1)观察统计图,写出两条你从这个统计图中获得的信息;
(2)请根据图中提供的数据,绘制折线统计图;
(3)如果要反映这六天最高气温的变化,采用条形统计图还是折线统计图更好,为什么?
|
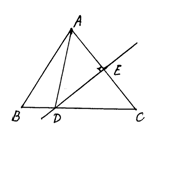 27.如图,在△ABC中,DE是AC的垂直平分线,△ABC与△ABD的周长分别为18cm和12cm,求线段AE的长.
27.如图,在△ABC中,DE是AC的垂直平分线,△ABC与△ABD的周长分别为18cm和12cm,求线段AE的长.
28.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称. (1)画出直线EF;(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN、EF所夹锐角![]() 的数量关系.
的数量关系.
|
五、(8分)
29.
|
(1)当三角板旋转到如图①的位置时,三角板的两边与等腰三角形的两底边分别相交于M、N两点,求证:AM=AN;
|
|
| |
六、(10分)
30.如图,已知直线![]() 与
与![]() 轴交于A点,与
轴交于A点,与![]() 轴交于B点,点M的坐标为(4,0),点P(
轴交于B点,点M的坐标为(4,0),点P(![]() ,
,![]() )是第一象限内直线AB上的动点,连接OP、MP. 设△OPM的面积为s.
)是第一象限内直线AB上的动点,连接OP、MP. 设△OPM的面积为s.
(1)求s关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的取值范围;
的取值范围;
(2)当P点在什么位置时,图中存在与△OPM全等的三角形?画出所有符合条件的示意图,并说明全等的理由(不能添加其他字母和其他辅助线);
|
参考答案
1.5,六次;2.-3; 3.四;4.略;5.![]() ;6.5;7.PA=PB=PC; 8.55°、55°或70°、40°; 9.5;10.②,不是轴对称图形; 11.
;6.5;7.PA=PB=PC; 8.55°、55°或70°、40°; 9.5;10.②,不是轴对称图形; 11.![]() ,
,![]() ,(3,0);12.
,(3,0);12.![]() ;13.B;14.B;15.C;16.D;17.A;18.A.;19.D;20.D;21.
;13.B;14.B;15.C;16.D;17.A;18.A.;19.D;20.D;21.![]() ; 22.
; 22.![]() ; 23.
; 23.![]() ,-8020;24.略;25.略;26.(1)(2) 略,(3)折线统计图,因为折线统计图能更好表示温度变化情况; 27.3cm; 28.(1)略(2)
,-8020;24.略;25.略;26.(1)(2) 略,(3)折线统计图,因为折线统计图能更好表示温度变化情况; 27.3cm; 28.(1)略(2)![]() ;29.略;30.(1)S=
;29.略;30.(1)S=![]() ,0<
,0<![]() <8(2)当∠BOP=∠MOP或PM⊥OA时,OPM≌APM.证明略 (3)P点坐标为(
<8(2)当∠BOP=∠MOP或PM⊥OA时,OPM≌APM.证明略 (3)P点坐标为(![]() ,
,![]() )和(4,2).
)和(4,2).
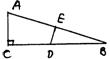


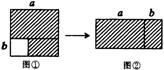

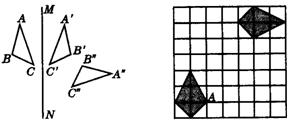
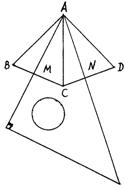
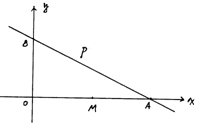 图1
图1