华师版八年级数学相似三角形复习练习
一、【方法指导与教材延伸】
1．在数学上，把具有 形状的图形称为相似形。
2．在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫做
，简称 。
3.已知四条线段a、b、c、d，如果a∶b＝c∶d，那么a、b、c、d叫做组成比例的 ，线段a、d叫做比例 ，线段b、c叫做比例 ，线段d叫做a、b、c的 。
比例中项：如果比例内项是两条相同的线段，即 ，那么线段b叫做线段a和c的比例中项。
4. 比例的性质：a∶b＝c∶d
；a∶b＝b∶c
5．两个相似形的特征：对应边成比例，对应角相等；
6．识别两个多边形是否相似的方法：如果两个多边形 ，那么这两个多边形相似
7．相似三角形：
定义： 的三角形叫相似三角形。如△ABC与△A/B/C/相似，
记作: 。
相似比：相似三角形 的比叫相似比，若△ABC∽△A/B/C/，相似比为k，则△A/B/C/与△ABC的相似比是 。即相似比是有顺序的。
8．相似三角形的识别方法：
(1)定义法： 的两个三角形相似。
(2)平行线法：
的直线和其它两边(或两边的延长线) ，所构成的三角形与原三角形相似。
注意：适用此方法的基本图形，(简记为A型，X型)
∵ED∥BC，∴△ABC∽△AED
(3) 的两个三角形相似。
(4) 的两个三角形相似。
(5) 的两个三角形相似。
(6) 对应成比例的两个直角三角形相似。
(7)被斜边上的高分成的两个直角三角形与原直角三角形相似。
3．相似三角形的识别方法的选择：
(1)已知有一角相等时，可选择方法 和方法 ；
(2)已知有二边对应成比例时，可选择方法 和方法 ；
(3)若有平行条件时，可考虑方法 ；
(4)有直角三角形时，可考虑方法
4.相似三角形的性质
(1)相似三角形的对应角相等，对应边成比例．
(2)相似三角形对应 的比、对应 的比、对应角 的比都等于相似比．
(3)相似三角形 的比等于相似比．
以上各条可以概括为：相似三角形的对应 之比等于相似比．
(4)相似三角形面积之比等于 ．
5．相似三角形性质的作用
综合使用相似三角形的性质与相似三角形的识别可以解决以下问题：
(1)可用来证明线段成比例、角相等、线段相等、垂直、平行等；
(2)可用来计算周长、边长、角度等；
(3)用来证明线段的平方比、图形面积的比等。
注意：
(1)求三角形某边长，可根据相似三角形的性质，得到对应线段成比例，再利用方程的思想方法，解出所求线段．
(2)有关三角形或其它图形面积的题目，常用到两个知识点：一、是三角形面积公式：S＝
底×高，这里特别注意图形中“同高”这个隐含条件，二、是相似三角形的面积比等于相似比的平方。
3．直角三角形中的比例线段是这部分内容的一个重点．如图，
由Rt△ACD∽Rt△CBD∽Rt△ABC，得
AC2＝AD·AB，
BC2=BD·AB，
CD2=AD·DB．
熟记这三个等式有时会给解题带来很大的方便，
尤其解几何综合题更明显，但须注意，在使用它们时，一定要证明这三个直角三角形相似．
二 、例题选讲
例1：已知线段a＝15厘米，b＝20厘米，c＝75毫米，d＝0.1米，问这四条线段成比例吗？
说明：在线段求比时，线段的长度单位要统一；要同单位下，两线段的比值是无单位的正数。
例2：已知线段a＝7，b＝4，求线段a＋b与a－b的比例中项。
说明：
(1)此处是求线段的比例中项，所以只能取正值，但实际上，比例中项并不一定都是指两条线段，两个数、两个字母同样也可以求出它们的比例中项，并且比例中项也可为负。
(2)所以在求比例中项时，一定要看清是求线段的比例中项，还是两个数的比例中项，它们的结果不一样的。
例3：已知
，且3x＋4z－2y＝40，求x、y、z的值。
说明：设k法是有关比例式计算题中常用的方法，应学会、掌握。
例题4：判断正误，并简要说出理由
(1)两个矩形一定相似。 ；
(2)两个菱形都有一个角是400，那么这两个菱形相似
(3)两个正方形一定相似。
(4)有一个角相等的两个等腰梯形相似。
例题5：如图，E、F分别为矩形ABCD的边AD、BC的中点，若矩形ABCD与矩形EABF相似，AB＝1，求矩形ABCD的面积
说明：运用相似多边形特征解题，应注意确定对应边、对应角，这里的AB是大矩形的宽，那么它只能中小矩形的长，大矩形宽与长的比等于小矩形宽与长的比。
例题6：(1)、如图，DE∥BC，EF∥AB，则图中相似形三角形有 对，分别是 。
(2)、如果AD＝5，DB＝3，FC＝2，则△ADE与△ABC的相似比是 ；
如何求出BF的长？
例题7：如图，在四边形ABCD中，E是对角线BD上的一点，EF∥AB，EM∥CD，
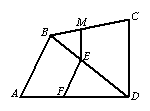求
的值。
例题8：如图，在△ABC中，AD⊥BC，BE⊥AC，则图中有 对相似三角形，
当△ ∽△ 时，则有
；
要 AC·CE＝CB·CD，则应找哪两个三角形相似？
解：
例题9：如图，在△ABC中，AB＝AC，AD是中线，P是AD上一点，过点C作
CF∥AB，延长BP交AC于点E，交CF于点F，说明：BP2＝PE·PF。
解：
 |
说明：当成比例的四条线段在同一直线上时，可用相等的线段代换的方法来分散开来，后再找相似三角形
例10．如图，在△ABC中，DE∥FG∥BC，并将△ABC分成三块S1、S2、S3，
若S1︰S2︰S3＝1︰4︰10，BC＝15，求DE、FG的长
 |
例11如图，在△ABC中，D是BC边上的中点，且AD＝AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F。
(1)说明：△ABC∽△FCD
(2)若S△FCD＝5，BC＝10，求DE的长。
三 【同步练习】
练习一
一、判断题：
1．所有的三角形都相似； 2．所有的梯形都相似；
3．所有的等腰三角形都相似； 4．所有的直角三角形都相似；
5．所有的矩形都相似； 6．所有的平行四边形都相似；
7．大小的中国地图相似； 8．所有的正多边形都相似。
二、填空：
1．延长线段AB到C，使BC＝AB，则AC︰AB＝ ，AB︰BC＝ ，BC︰AC＝
2．在比例尺为1︰500000的地图上，量得甲、乙两地的距离是25㎝，则两地的实
际距离是 。
3．已知点P在线段AB上，且AP︰PB＝2︰5，则AB︰PB＝ ，AP︰AB＝
4．如图，已知
，AD＝15，AB＝40， AC＝28，则AE＝ 。
5．已知：线段a＝3，b＝2，c＝4，则b、a、c的第四比例项d＝ ；
则a、b、(a－b)的第四比例项是 ；3a、(2a－b)的比例中项是 。
6．已知：数3、6，请再写出一个数，使这个数是另外两个数的比例中项，这个
数是 。
7．已知：
则
。
8．已知
，且3y＝2z＋6，则x＝ 、y＝ 。
9．把一个矩形的硬纸片剪去一个正方形，若剩下的矩形与原矩形相似，那么原
矩形的长边和短边之比为 。
三、判断下列各组线段是否成比例？
1．4㎝、6㎝、8㎝、2㎝； 2．1.5㎝、4.5㎝、2.5㎝、7.5㎝
3．1.1㎝、2.2㎝、3.3㎝、6.6㎝； 4．2㎝、4㎝、4㎝、8㎝。
四、解答题：
1．已知：3x－5y＝0，求：(1)
；(2)
；(3)
2．已知：x︰y︰z＝2︰3︰4，求：
的值。
练习二
一、填空：
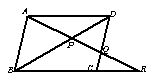
1、如图(1)，在 中，R在BC的延长线上，AR交BD于P，交CD于
Q，若DQ∶CQ＝4∶3，则AP∶PR＝
 | |||||||
 | |||||||
 | |||||||
 | |||||||
图(1) 图(3) 图(4)
2、如图(2)，在梯形ABCD中，CD∥AB，AC、BD交于点O，过点O作AB的平行线交AD于点E，交BC于点F，则图中有 对相似形三角形；若DC＝9，AB＝15，则OD∶OB＝ ，EF＝ 。
3、如图(3)，在△ABC中，∠BAC＝900，CE平分∠ACB，AD⊥BC，垂足为D，AD、CE相交于点F，则△AFC∽△ 。
4、如图(4)，要使△AEF∽△ABC，已具备的条件是 ，还需补充的条件是 或 或 。
5、如图(5)，点D是△ABC内一点，连结BD并延长到E，连结AD、AE，若∠BAD＝200，
，则∠EAC＝
 |
图(5) 图(6)
6、在△ABC中，AD⊥BC，DE⊥AB，则有AD2＝ ，ED2＝ ，BD2＝ 。
若DF⊥AC，则还有线段 是比例中项。
二、解答题：
1、如图(1)，在 中，对角线AC、BD相交于点O，BC＝18，E为OD的中点，连结CE并延长交AD于点F，求DF的长。
 |
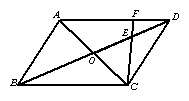2、如图(3)，在△ABC中，E、F分别是AC、BC的中点，AF与BE交于点O，ED∥AF，交BC于点D，求BO∶OE的值。
 |
3、如图，AE2＝AD·AB，且∠ABE＝∠C，试说明△BCE∽△EBD。
 |
4、如图，已知
，试说明：AB·EC＝AC·BD。
5、如图，D是△ABC内一点，在△ABC外取一点E，使∠CBE＝∠BAD，试说明△ABC∽△DBE
 |
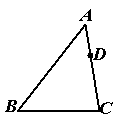
6、如图，在△ABC中，AB＝8，AC＝6，点D在AC上，AD＝2，试在AB上求一点E，使△ADE和△ABC相似，并求出AE的长。
 |
7、如图，在直角梯形ABCD中，AB＝7，AD＝2，BC＝3，如果边AB上的点P使得以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似，则这样的P点有 个
 |
8、如图，点C、D在线段AB上，△PCD是等边三角形，
①当AC、CD、BD满足怎样的关系时，△ACP∽△PDB？
②当△ACP∽△PDB时，求∠APB的度数。
 |
练习三
一、填空：
1．如果两个相似三角形对应高的比为4:5，那么它们的面积比为
2．把一个三角形变成和它相似的三角形，而面积扩大为原来的100倍，则边长扩大为原来的 倍。
3．如果两个相似三角形的面积比为8，周长比为k，那么
＝ 。
4．在△ABC中，DE∥BC，
，且S△ABC＝8cm2，那么S△ADE＝ cm2
5．如图(2)，C为线段AB上的一点，△ACM、△CBN都是等边三角形，若AC＝3， BC＝2，则△MCD与△BND的面积比为 。
6．如图(3)，在△ABC中，D、E分别是AB、AC的中点，则△ADE与四边形DECB的面积之比为 。
7．如图(4)，DE∥FG∥BC，且S△ADE＝S梯形DFGE＝S梯形FBCG，则DE:FG＝ 。
8．如图(5)，在梯形ABCD中，AD∥BC，AC、BD交于O点，S△AOD:S△COB＝1:9，
则S△DOC:S△BOC＝
二、解答：
1、在△ABC中，∠C＝900，BC＝8㎝，AC︰AC＝3︰5，点P从点B出发，沿BC向点C以2㎝/s的速度移动，点Q从点C出发沿CA向点A以1㎝/s的速度移动，如果P、Q分别从B、C同时出发：
⑴经过多少秒△CPQ∽△CBA？
⑵经过多少秒时，以C、P、Q为顶点的三角形恰与△ABC相似
 |