八年级数学上册月考试题
一、填空题：（3×10）
1．如图，直线a∥b，∠1=130°，则∠2= 度．
2．在等腰三角形ABC中，AB=AC，若∠B=40°，则∠A= ，∠C=
。
3．等边三角形有 条对称轴。
4．Rt⊿ABC的斜边长为6cm,则斜边上的中线长为 cm.
5.已知两条线段的长为5 cm和12 cm，当第三条线段的长为 cm时，这三条线段就能组成一个直角三角形。
6．直角三角形一条直角边长与斜边长分别为8 cm和10 cm，则斜边上的高等于 cm。
7．如图，若AD∥BC，AB∥DC，∠A=63°，则∠C= 。
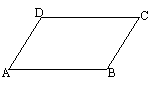8．已知：如图， AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DEF的平分线相交于点P．∠P= ．
9．等腰三角形的两边长分别为7cm和4cm，则它的周长为________.
10.将一根16 cm长的细木棒放入长、宽、高分别为4 cm，3 cm和12 cm的长方形无盖盒子中，则细木棒露在盒外面的最短长度是 cm。
二、选择题：（3×10）
11．如果∠α和∠β是同位角，且∠α=55°则∠β等于 （ ）
A．55° B。125° C。55°或125° D。无法确定
12．下列图形中，不一定是轴对称图形的是 （ ）
A．线段 B．角 C．直角三角形 D．等腰三角形
13．根据下列条件不能判定两个直角三角形全等的是（ ）
A．两条直角边对应相等 B．一个锐角和斜边对应相等
C．斜边和一条直角边对应相等D．两个锐角对应相等
14．如图所示，△ABC中，AB=AC，过AC上一点作DE⊥AC，EF⊥BC，若∠BDE=140，°则∠DEF=（ ）
（A）55° （B）60° （C）65° （D）70°
15．下列能断定△ABC为等腰三角形的是（ ）
（A）∠A=30º、∠B=60º （B）∠A=50º、∠B=80º
（C）AB=AC=2，BC=4 （D）AB=3、BC=7，周长为13
16．等腰三角形的顶角等于70o，则它的底角是 ( )
A、70o B、55o C、 60o D、 70o或55o
17．下列说法中，正确的有 （ ）
①有一个角为60°的等腰三角形是等边三角形
②三边分别是1， 
，
3的三角形是直角三角形
③一边上的中线等于这条边的一半的三角形是直角三角形
④三个角之比为3：4：5的三角形是直角三角形
⑤到角两边距离相等的点，在这个角的平分线上
A．1个 B．2个 C．3个 D．4个
18．下列说法正确的是（ ）
A．同位角相等B．内错角相等C．对顶角相等 D．同旁内角互补
19．已知等腰△ABC的底边BC=8cm，且│AC-BC│=2cm，那么腰AC的长为（ ）
A．10cm或6cm B、10cm C、6cm D、8cm或6cm
20．正三角形ABC所在平面内有一点P，使得⊿PAB、⊿PBC、⊿PCA都是等腰三角形，则这样的P点有（ ）
（A）1个 （B）4个 （C）7个 （D）10个
三．解答题（60分）
21．（6分）如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知),∴∠1=∠3( ),
∵∠1=∠2(已知),∴∠2=∠3( ),
∴________∥________( ),
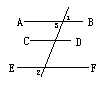∴∠3+∠4=180°(
).
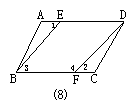
22．（8分）如图,已知∠1=∠2,AB∥CD,求证:CD∥EF.
23．（6分）如图，已知：在
中，
，
，BD是 的角平分线，求
的度数.
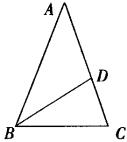
24．（8分）如图，已知∠EAC是△ABC的外角，∠1=∠2，AD∥BC，请说明AB=AC的理由。
 |
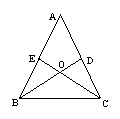
25．（8分）如图，
中，AB=AC，2条角平分线BD、CE相交于点O。
（1）OB与OC相等吗？请说明你的理由；
（2）若连接AO，并延长AO交BC边于F点。你有哪些发现？请写出两条合乎情理的发现，并就其中的一条发现写出推理过程来证实你的发现。
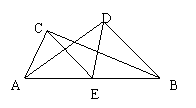26．（8分）如图，△ABC和△ABD中，AC⊥BC，AD⊥BD，E是AB边上的中线。试判断DE与CE是否相等，并说明理由。
27．（8分）“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过
千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪正前方
米处，过了
秒后，测得小汽车与车速检测仪间距离为
米，这辆小汽车超速了吗？
 |
28．（8分）在Rt⊿ABC中，∠C=90°，∠A、∠B、∠C的对边长分别为a、b、c，设⊿ABC的面积为S，周长为l.
(1)填表：
| 三边长a、b、c | a+b-c |
|
| 3、4、5 | 2 | |
| 5、12、13 | 4 | |
| 8、15、17 | 6 |
（2）如果a+b-c=m，观察上表猜想：
= ，（用含有m的代数式表示）。
（3）说出（2）中结论成立的理由。