初二数学第一学期第一次月月清考试
初二数学试题
（时间：90分钟 总分：100分 命题人：张德建）
一、选择题： （2分×8+3分×4=28分）
1、下列函数y=πx y=3-2x y= y=x2-2 ，其中一次函数共有 ( )
A、 1个 B、2个 C、3个 D、4个
2、函数y= 的自变量x的取值范围是 ( )
A、x≠2 B、x≥3 C、x>3且x≠2 D、x≥3且x≠2
3、点（1，2）在下列哪个函数图象上 ( )
A、y=x-3 B、y=2x+2 C、y= D、y=x2+2
4、如果想了解每组数据相对于总数的大小应选择 ( )
A、条形图 B、扇形图 C、折线图 D、直方图
5、已知ΔABC和ΔDEF中，∠B=∠E BC=EF，还需要补充一个条件才能使ΔABC≌ΔDEF，其中补充错误的是 ( )
A、∠A=∠D B、∠C=∠F C、AB=DE D、AC=DF
6、一次函数y=(m-2)x+3-m的图象不经过第四象限，则 ( )
A、m>2 B、m<3 C、2<m<3 D、2<m≤3
7、在直方图中，其中某一小组的高度等于其他小组的高度之和，则这小组的频率为 ( )
A、0.25 B、0.30 C、0.50 D、0.80
8、如图： △AEC ≌△OFC AD=7 BC=5 则AB= ( )
A、3cm B、2cm C、1cm D、无法求出
9、一个容量为80的样本最大值是141, 最小值是50, 取组距10,则可以分为 ( )
A、10组 B、9组 C、8组 D、7组
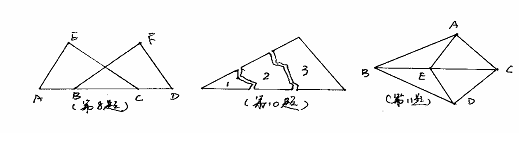
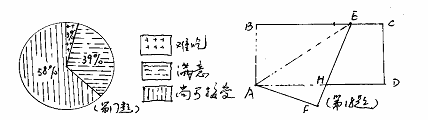
10、某同学把一块三角形的玻璃打成了3块，现要到玻璃店去配一块 完全一样的玻璃那么最省事的是 ( )
A、带① B、带② C、带 ③ D、①②③都带去
11、 如图，AB=BD，AC=DC，E是BC上一点，则图中的全等三角形只有 ( )对
A、0 B、1 C、2 D、3
12、 △ABC中，AB=7，AC=3，AD点中线，则AD的取值范围是 ( )
A、4＜AD＜10 B、3＜AD＜7
C、2＜AD＜5 D、 3＜AD＜5
二、填空题(3'×6=18')
13、将直线y= 2x-5 向上平移7个单位所得的直线的解折式为_________________.
14、一次函数y=kx+b 中y 随x 的增大而减小且过点(1, -3) ，则其解折式为：______________________. (写出一个即可)
15、一次函数y=kx+b，过点(0,2)，且x 增大1时y增大3，则其解析式为_____________________.
16、某校八年级(1)班学生年龄为14、15、16岁三种，其中人数之比为3:5:2，其中14岁的有15人，则这个班16岁的有_________人。
17、我校就师生对食堂伙食的满意程度进行了调查，如图所 示，据此可估计我校师生对食堂伙食表示认可的占___________.
18、如图，将长方形ABCD纸张折叠，得到如图所示的图形，已知∠AHF=80°,
则∠AEB=______________
三、解答题
19、(6' ) 已知一次函数图象经过(3，5) 和(-4，-9)两点，
⑴求此一次函数解析式 ⑵若点(a, -3)在此函数图象上，求a的值
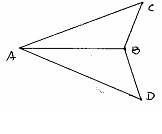
20、(6' )如图：AC=AD，BC=BD，图中有相等的角吗？请找出来，并说明你的理由。
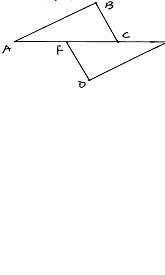
21、如图：BC=BF，AF=EC。请补充一个条件____________(写一个即可)，使ΔABC≌ΔEDF，并加以证明。
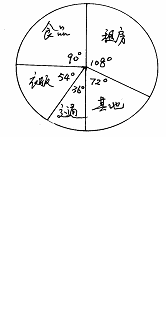
22、(8') 如图为已故英国王妃戴安娜的消费模式，其中她每月在衣服上花费为4200英磅
⑴求她每月的租房的费用
⑵求她每月的总消费
⑶请你制作一个统计图，形象地表示戴安娜每月的消费。
23、(8')已知函数y1=x-1和 y2 =-2x+3
⑴在所给的平面直角坐标系内画出这两个函数的图象
⑵求这两条直线的交点坐标
⑶观察图象，当x 在什么范围内时y1 ＜y2
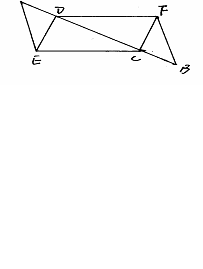
24、(8')如图A、D、C、B在一直线上，AD=BC，AE=BF，CE=DF，
求证： ⑴DF∥CE ⑵DE=CF
25、(10)某饮料厂现有A种原料70公斤，B种原料52公斤。现计划用这两种原料生产甲、乙两种品牌的饮料共80桶，已知做一桶甲种饮料需A种原料0.6公斤，B种原料0.9公斤，可获利45元；做一桶乙种饮料需A种原料1.1公斤，B种原料0.4公斤，可获利50元。设生产甲种饮料x桶，用
这批原料生产的两种品牌的饮料的总利润为y元。 ⑴求y与x 之间的函数关系式，并求自变量的取值范围。 ⑵如何安排生产才能使该厂在生产这批饮料中获利最大。
26、(10')如图，平面直角坐标中，AB⊥BC，DC⊥BC，垂足分别为B、C两点，OA⊥OD，OC=AB，⑴求证：DC=OB； ⑵若点A为正比例函数 y= x 的图象上一点，且横坐标为6，求OD所在的直线的解析式。