初二年级第二学期第一次月考

![]() 数 学 试 卷
数 学 试 卷
(满分150分.时间100分钟)
温馨提示: 请仔细审题,细心答题,相信你一定会有出色的表现!
试 卷 Ⅰ(选择题共48分)
一、相信你的选择(本题有12个小题,每小题4分,共48分)下面每小题给出的四个选项中,有且只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内。
1.在有理式![]() 中,分式有………( ).
中,分式有………( ).
A. 1个 B. 2个 C. 3个 D. 4个
2.分式![]() 中的
中的![]() 同时扩大2倍,则分式的值………………………………( ).
同时扩大2倍,则分式的值………………………………( ).
A. 不变
B. 是原来的![]() C. 是原来的4倍 D. 是原来的2倍
C. 是原来的4倍 D. 是原来的2倍
3.一件工作,甲独做a小时完成,乙独做b小时完成,则甲、乙两人合作完成需要( )小时。
A. ![]() +
+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 4.
4. 
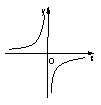
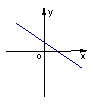 函数
函数![]() 的图象如图3所示,那么函数
的图象如图3所示,那么函数![]() 的图象大致是……( ).
的图象大致是……( ).
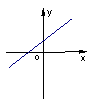
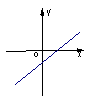
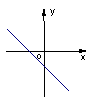
第4题图 A B C D
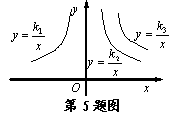 5.如图是三个反比例函数
5.如图是三个反比例函数![]() ,
,![]() ,
,![]() 在x轴
在x轴
上方的图象,由此观察得到![]() 、
、![]() 、
、![]() 的大小关系为(
)
的大小关系为(
)
A. ![]() B.
B. ![]()
C.
![]() D.
D. ![]()
6.
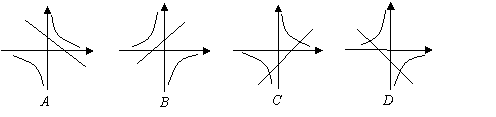 函数
函数![]() 与
与![]() 在同一平面直角坐标系中的图像可能是………( )。
在同一平面直角坐标系中的图像可能是………( )。
7. 学生有![]() 个,若每
个,若每![]() 个人分配1间宿舍,则还有一人没有地方住,问宿舍的间数为( ).
个人分配1间宿舍,则还有一人没有地方住,问宿舍的间数为( ).
A.
![]() B.
B.
![]() C.
C.![]() D.
D.![]()
8.张老师和李老师同时从学校出发,步行15千米去县城购买书籍,张老师比
李老师每小时多走1千米,结果比李老师早到半小时,两位老师每小时各走多
少千米?设李老师每小时走x千米,依题意,得到的方程是 …………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() ,则
,则![]() 的值为 ……………………………………………(
)
的值为 ……………………………………………(
)
A.
![]() B.
B. ![]() C.
C. ![]() D. ―
D. ―![]()
10.若分式方程![]() +
+![]() =
=![]() 有增根,则增根可能是………………( )
有增根,则增根可能是………………( )
A. a B. b C. a和b D. a或b
11.已知![]() ,
,![]() ,则M与N的大小关系为……( ).
,则M与N的大小关系为……( ).
A. M>N B. M=N C. M<N D. 不能确定
12.学校计划将120名学生平均分成若干个学习小组,若每个小组比原计划多一个人,则要比原计划少分出6个小组,那么原计划要分成的小组数是 …………………………………( ) A.40 B.30 C.24 D.20
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
试 卷 Ⅱ(非选择题共102分)
二、填空题(本题有8个小题,每小题4分,共32分)
13.①在分式![]() 中,当x=
时,分式无意义.
中,当x=
时,分式无意义.
②在分式![]() 中,当a=
时,分式的值为零.
中,当a=
时,分式的值为零.
14.①若![]() ,则
,则![]() 的值是
,②化简
的值是
,②化简![]() -
-![]() =
=
15.人体中成熟的红细胞的平均直径为0.m,用科学记数法可表示为 mm.
16.不改变分式的值,
①使它的分子与分母中最高次项的系数都为正数,则![]() =
.
=
.
②使它的分子与分母中各项系数都化为整数,则![]() =
.
=
.
17. 已知函数y=(m-1)xm2-5是反比例函数,且它的图象在第一、三象限,那么m=
18. 已知圆柱的侧面积是6πcm2,若圆柱的底面圆的半径为x(cm),高为y(cm),则y与x的函数关系式是
19. 已知函数y=- 在第一象限的图象如图8所示,点P为图象上的任意一点,过P作PA⊥x轴于A,PB⊥y轴于B,则△APB的面积为 .
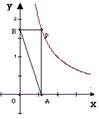
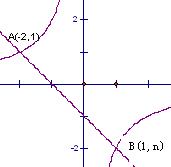
20.如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(-2,1)、B(1,n)两点,根据图象可以知道:一次函数的值大于反比例函数的值的X的取值范围是
的图象交于A(-2,1)、B(1,n)两点,根据图象可以知道:一次函数的值大于反比例函数的值的X的取值范围是
三、计算题(本大题共18分)
21.(本题10分)先化简代数式![]() ,然后请选择一组你喜欢的
,然后请选择一组你喜欢的![]() 的值代入求值.
的值代入求值.
22.(本题8分)解方程:![]()
四、拓广探索(本大题共12分)
23.(本题12分)
小明在计算![]() ,
,![]() ,
,![]() ,…时发现
,…时发现![]() ,
,![]() ,
,![]() ,…
,…
(1)用式子表示这一变化规律;
(2)利用这一规律计算:
![]()
五.解答题:(本大题共4小题,共40分。解答应写出文字说明、证明过程或演算步骤。)
24.(10分)已知函数y = y1-y2,y1与x成反比例,y2与x-2成正比例,且当x = 1时,y =-1;当x = 3时,y = 5. ①求Y与X的函数关系式?②求当x=5时y的值。
25. (10分)某校师生到距学校20千米的公路旁植树,甲班师生骑自行车先走,45分钟后,乙班师生乘汽车出发,结果两班师生同时到达,已知汽车的速度是自行车速度的2.5倍,求两种车的速度各是多少?
26.(10分)如下图,点A、B在反比例函数的图象上,且点A、B的横坐标分别为a,2a(a>0),AC⊥x轴,垂足为点C,且△AOC的面积为2。
(1)求该反比例函数的解析式。
 (2)若点(-a,y1),(-2a,y2)在该反比例函数的图象
(2)若点(-a,y1),(-2a,y2)在该反比例函数的图象![]() 上,试比较y1与y2的大小。
上,试比较y1与y2的大小。
27.(10分)一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则经过6小时可到达乙地。
(1)甲、乙两地相距多少千米?
(2)如果汽车把速度提高到y(千米/时)那么从甲地到乙地所有时间x(小时)将怎样变化?
试写出y与x之间的函数关系式:
(3)因某种原因,这辆汽车需在5小时内从甲地到达乙地,则此时汽车的平均速度至少应是多少?
(4)已知汽车的平均速度最大可达80千米/时,那么它从甲地乙地最快需要多长时间?
第二学期初二年级第一次月考
数 学 试 卷 参 考 答 案
试卷Ⅰ(选择题共48分)
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | D | C | B | C | C | B | B | D | B | B |
试卷Ⅱ(非选择题共72分)
二、填空题(本题有8个小题,每小题4分,共32分)
13.①x= 2或-2 . ②a= -3 .
14.①![]() ,②
,② ![]()
15.7.7×10-6 mm. 16.①![]() . ②
. ②![]() .
17. m=2
.
17. m=2
18.![]() 19.
19. ![]() 20. x<-2, 0<x<1
20. x<-2, 0<x<1
三、计算题(本大题共18分)
21. ![]()
=![]() …………………………………………(2分)
…………………………………………(2分)
=![]() …………………………………………(3分)
…………………………………………(3分)
=![]() …………………………………………(4分)
…………………………………………(4分)
=![]() …………………………………………(5分)
…………………………………………(5分)
=![]() …………………………………………(6分)
…………………………………………(6分)
求值根据具体情况:①看选择的![]() 的值是否有意义,②代入时是否正确.
的值是否有意义,②代入时是否正确.
计算结果正确 …………………………………………(10分)
22.(本题8分)解方程:![]()
解:去分母得:(x+1)2-4=x2-1 ………………………………………(3分)
整理得 2x=2
x=1 ………………………………………(5分)
检验: 将 x=1 代入分母(x+1)(x-1)=0
x=1是增根 ………………………………………(7分)
所以 原方程无解 ………………………………………(8分)
四、拓广探索(本大题共12分)
23.(本题12分)
(1)用式子表示这一变化规律;![]() ………………………………(4分)
………………………………(4分)
(2)利用这一规律计算:
![]()
=![]()
=![]()
=![]()
五.解答题:(本大题共4小题,共40分。解答应写出文字说明、证明过程或演算步骤。)
24.(10分)已知函数y = y1-y2,y1与x成反比例,y2与x-2成正比例,且①求Y与X的函数关系式?②求当x=5时y的值。
解:①由题意 令![]() ,y2 =
,y2 =![]() (
(![]() -2)
-2)
∵ y = y1-y2 ∴ y =![]() -
-![]() (
(![]() -2)
-2)
∵当x = 1时,y =-1;当x = 3时,y = 5.
∴ -1=K1+K2
5 =![]() -
-![]()
∴![]() = 3
= 3
![]() =-4
=-4
② 当x=5时,y=![]() +4×(5-2)=
+4×(5-2)=![]()
25. 解:设自行车的速度为x km/h,则汽车的速度是2.5x km/h,
由题意![]() 即
即
![]()
去分母 3x=48 x=16
经检验知x=16 是原方程的解
∴ 2.5x=40
答 自行车速度是16 km/h,则汽车的速度是40 km/h,
26.分析:通过Rt△AOC的面积![]() ,可知xA·yA=4。又因为点A在双曲线上,所以xA·yA=k,可求出函数的解析式,再根据反比例函数的性质,k<0,y随x的增大而增大知,自变量x越大,函数值反而小,通过比较-a与-2a的大小可知y1与y2的大小。
,可知xA·yA=4。又因为点A在双曲线上,所以xA·yA=k,可求出函数的解析式,再根据反比例函数的性质,k<0,y随x的增大而增大知,自变量x越大,函数值反而小,通过比较-a与-2a的大小可知y1与y2的大小。
解:(1)因为点A在反比例函数![]() 的图象上,设A点的坐标为(
的图象上,设A点的坐标为(![]() ,
,![]() )。………(2分)
)。………(2分)
∵a>0,k<0,∴AC=-![]() ,OC=
,OC=![]() ,
,
又∵S△AOC=![]() ……………………………………(4分)
……………………………………(4分)
∴![]() , k=-4,
, k=-4, ![]()
即反比例函数的解析式为![]() 。
……………………………………(6分)
。
……………………………………(6分)
(2)∵A点,B点横坐标分别为a,2a(a>0)
∴2a>a,即-2a<-a<0
由于点(-a,y1),(-2a,y2),在双曲线上,根据反比例函数的性质k<0,y随x增大而增大知y1>y2。 ……………………………………(10分)
27.解:(1)甲、乙两地的相距是 50×6=300千米
(2)y随x增大而减小, y与x之间的函数关系式是:![]()
(3)如果这辆汽车需在5小时内从甲地到达乙地,那么汽车的平均速度至少应是60千米/时,
(4)汽车的平均速度最大可达80千米/时,那么它从甲地乙地最快需要3.75小时