八年级 数学 第三学月检测题
（内容：第五章 位置的确定 第六章 一次函数）
 |
时间：120分钟 总分：150分
一、精心选一选(（本大题共10小题，每小题4分，满分40分)
1、下列函数（1）y=
(2)y=2x-1
(3)y=
(4)y=2-1－3x (5)y=
中，是一次函数的有（ ）
A． 4个 B. 3个 C. 2个 D. 1个
2、点P关于x轴的对称点
的坐标是（4，－8），
则P点关于原点的对称点
的坐标是（ ）
A.（－4，－8） B.（4，8） C.（－4，8） D.（4，－8）
3、已知P（x，y）在第四象限，且x=3，y=5，则P点坐标为（ ）
A.（3，5） B.（-3，5） C.（3，-5） D.（-3，-5）
4、对于正比例函数y=mx，y随着x的增大而增大，则m的取值范围（ ）
A. m＜0 B. m≤0 C. m＞0 D. m≥0
5、下面哪个点不在函数y=－2x+3的图象上（ ）
A.（-5，13） B.（0.5，2） C.（3，0） D.（1，1）
6、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h
(厘米)与燃烧时间t(时)的函数关系的图象是( )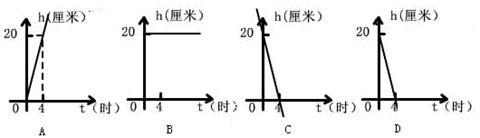
7、点P（m+3,m+1）在直角坐标系的y轴上，则P点坐标为（ ）
A. (0,-2) B. (2,0)
C. (4,0) D. (0,-4)
8、点P(3，m)到x轴的距离是4,则m的值为（ ）
A. 4 B.±4 C.－4 D.无法确定
9、直角坐标系中，A、B两点的横坐标相同但均不为零，则直线AB（ ）
A. 与x轴平行 B. 与y轴平行
C. 经过原点 D.不能确定
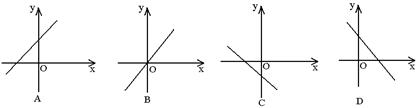
10、 如图所示图象中，不可能是关于x的一次函数y=mx-(m-3)
的图象的是( )
 |
二、细心填一填(本大题共10小题，每小题3分，满分30分)
11、电影院的8排10号用（8、10）表示，那么10排8号可用 表示。
12、某商店出售一种瓜子，其售价y（元）与瓜子质量x（千克）之间的
关系如下表：
| 质量x（千克） | 1 | 2 | 3 | 4 | …… |
| 售价y（元） | 3.60+0.20 | 7.20+0.20 | 10.80+0.20 | 14.40+0.2 | …… |
由上表得y与x之间的关系式是 。
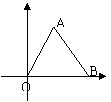13、如图，△AOB是边长为6的等边三角形,
则A，B两点的坐标分别是A ,
B ,OA所在直线方程为 。
14、当
时，函数
是正比例函数。
15、求下列各函数的自变量x的取值范围
（1） ；（2） ；
 |
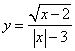（3） 。
16、如图所示，如果“士”所在位置的坐标是（－１，－２），
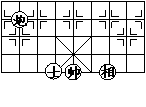“相”所在位置的坐标是（２，－２），
那么“炮”所在位置的坐标是 。
17、若点A（-2，3）先向右平移3个单位，
在向下平移1个单位，
得到的点的坐标为 。
18、一次函数y= -2x+4的图象与x轴交点坐标是 ，与y轴交点坐标是 ，图象与坐标轴所围成的三角形面积是 .
19、某汽车油箱中能盛汽油80升，汽车每行驶40千米耗油6升，加满油后，
油箱中剩余油量y（升）与汽车行驶路程x（千米）之间的函数关系式是 。
20、写出同时具备下列两个条件的一次函数表达式
（写出一个即可）__________________.（1）y随着x的增大而减小；
（2）图象经过点（1，-3）
 |
三、耐心做一做：(本大题共8题，共80分)
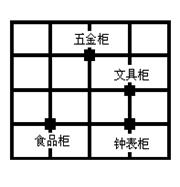
21、(10分)如图是重百商场的各个柜台分布平面示意图，
请建立合适的直角坐标系，标出各个柜台的坐标．
 |
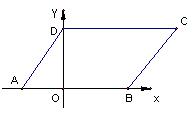
22、(10分)平行四边形ABCD，AD＝6，AB＝8，点A的坐标为（－3，0），
求B、C、D各点的坐标。
23、（10分)已知y与x成一次函数，当x=0时，y＝3，当x=2时，y=7。
（1）写出y与x之间的函数关系式。
（2）计算x＝4时，y的值。
（3）计算y＝4时，x的值。
24、(10分)某校组织学生到距离学校6千米的博物馆去参观，小磊准备乘出租车去，出租车的收费标准如下：3千米以下收费8元；3千米以上，每增加1千米，加收1.2元。
(1)写出出租车行驶的里程数x(x大于3千米)与费用y(元)之间的关系式。
(2)小磊只带10元钱，到博物馆够用吗？
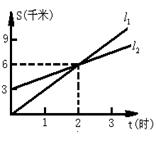
25、(10分)已知A地在B地正南方向3千米处，甲、乙两人分别从两地向正北方向匀速直行，他们与A地的距离S（千米）与所行时间t（小时）之间的关系如图所示，其中
表示甲运动的过程，
表示乙运动的过程，根据图象回答：
⑴ 甲和乙哪一个在A地，哪一个在B地？
⑵ 甲用多长时间追上乙？
⑶ 求出表示甲的函数关系和乙的函数关系式．
⑷ 通过函数关系式，说明什么时候两人又相距3千米？
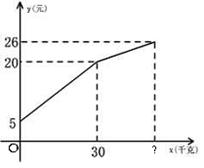
26、(10分)一农民带上若干千克自产的土豆进城出售,为了方便,他带了些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1 )农民自带的零钱是多少?
(２)降价前每千克的土豆价格是多少?
(３)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱
(含备用零钱)是26元,试问他一共带了多少千克土豆?
(４)试求y与x之间的关系式。
27、(10分)把蓄水量为Q（立方米）的水池中的水抽干，用每小时抽水量为k立方米的抽水机抽水，剩余水量P立方米和抽水时间t（时）之间的函数关系图象如图所示．
⑴ 写出Q的值． ⑵ 求出k的值．
⑶ 写出P与t之间的函数关系式．
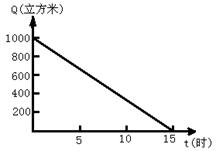⑷ 多少时间能将水池中的抽干？
28、(10分)重庆某电信运营商有两种手机卡，A类卡收费标准如下：无月租，
每通话1分钟交费0.6元；B类卡收费标准如下：月租费50元，每通话1分钟交费0.4元。
① 分别写出A、B两类卡每月应缴费用Y（元）与通话时间x（分）之间的关系式；
② 一个用户这个月预交话费200元，按A、B两类卡收费标准分别可以通话多长时间？
③ 若每月平均通话时间为300分钟，你选择哪类卡？
④ 每月通话多长时间，A、B两类卡的费用相同？
第三学月考试（第五章 位置的确定 第六章 一次函数）
一、1、C 2、A 3、C 4、C 5、C 6、D 7、A 8、B 9、B 10、C
二、11、（10,8） 12、y=3.6x+0.2 13、（3,3
）；（6,0）；y=-x +6
14、3 15、
16、（－3,1）
17、（1,2） 18、（2,0）；（0,4）；4 19、
20、y=-3x
21、画图略；
22、解：在Rt△ADO中，AO=6，
AO=3，
∴OD=
=
D(0，) B(
5，0) C(8，)
23、解：(1)设一次函数关系式为：y=kx+b (k≠0)
则
解方程组得: 
∴一次函数为：y=2x+3
(2)当 x=4时，y=2×4+3=11
(3)当y=4时，x=
24、解：(1)当
时，y=8
当x>3时，y=8+1.2(x-3)
化简得：y=1.2x+4.4
(2)∵6>3时
当x=6时 y=1.2×6+4.4=11.6
∵11.6>10 ∴到博物馆费用不够
25、（1）甲在A地，乙在B地
（2）2小时
（3）
甲=
，乙=
（4）由图得甲－乙=3，
，
即
， 4小时后又相距3千米。
26、解：(1)农民自带零钱为5元
(2)降价前每斤土豆为0.5元
(3)他一共带的土豆数为45千克
(4)当
,
当x>30时，
27、（1）Q=1000
（2）K=
（3）
（4）15小时
28、解：(1)
=50+0.4x
(2)当
=200元时，x=
当
=200元时，x=
∵
∴B类卡通话时间长
(3)若 x=300时
=0.6×300=180(元)
=0.4×300+50=170(元)
∵180>170 ∴选用B类卡
(4)因A、B两类卡的费用相同，则
0.6x=0.4x+50 x=250
∴每月通话时间为250分钟，两类费用一样