北师版八年级数学上册半期考试题
 |
时间：120分钟 总分：150分
一、精心选一选(（本大题共10小题，每小题4分，满分40分)
1、9的算术平方根是（ ）
A. 3
B. 
3
C. 
D.
2、在下列各数中无理数有（ ）
-0.333…，
，-
，3，3.1415，2.010101…（相邻两个1之间有1个0），76.…（小数部分由相继的正整数组成）。
A． 3个 B. 4个 C． 5个 D. 6个
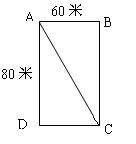3、如图,是我校的长方形水泥操场，如果
一学生要从A角走到C角，至少走（ ）
A. 80米 B. 90米
C. 100米 D. 110米
4、已知从多边形的一个顶点引出的对角线把多边形分为10个三角形，则此多边形内角和是( )
A.14400 B.18000
C.21600 D.16200
5、下列命题中，正确的是（ ）
A.矩形的对角线互相垂直
B.菱形的对角线相等
C.正方形的对角线互相垂直平分且相等
D.等腰梯形的对角线互相平分
6、以下五家银行行标中，是轴对称图形又是中心对称的有（ ）
A.1个 B.2个 C.3个 D.4个
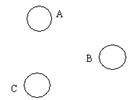7、体育课上，刘老师在篮球场上放置三个
不在同一直线上的A，B，C三个篮球，
现将篮球D放置其中，使A，B，C，D
四个篮球组成 一个平行四边形，试问
篮球D在图中位置有（ ）
A. 1处 B. 2处 C. 3处 D. 4处
8、下列四个图形中，不能通过图形平移得到的是（ ）
 |
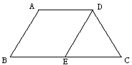9、如图，等腰梯形ABCD中，AD∥BC，AD=5，
AB=6，BC=8，且AB∥DE，
△DEC的周长是（ ）
A.3 B.12 C.15 D.19
10、如图，矩形ABCD沿AE折叠，使D点落在BC边上的F点处。
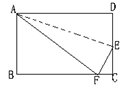如果∠BAF=60ο，则∠DAE等于（ ）
A.15
B.30
C.45
D.60
二、细心填一填(本大题共10小题，每小题3分，满分30分)
11、化简：（1）
= ，（2）
= ，（3）
= _ ____。
12、若
则
；若
，则
；
。
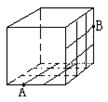
13、 如图所示一棱长为3cm的正方体，把所有的面
均分成3
3个小正方形。其边长都为1cm，
假设一只蚂蚁每秒爬行2cm，则它从下底面
点A沿表面爬行至侧面的B点，
最少要用 秒钟。
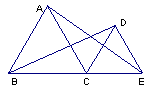14、△ABC和△DCE是等边三角形，则在此图
中，△ACE绕着 点逆时针方向
旋转 度可得到△ 。
15、菱形的面积为24㎝2，一对角线长为6㎝，则另一对角线长为 ，边长为 ，一组对边的距离为 。
16、A、B、C、D在同一平面内，从①AB∥CD；②AB=CD；③BC∥AD；
④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形
的选法有______种。
17、要把一个菱形判定为正方形,可添加的条件为_______________（只写一个条件）.
18、如图所示是某工厂厂房屋顶的人字架
（等腰三角形），它的跨度BC＝12米，
中柱AD为2.5米，中柱AD⊥BC，
且垂足D为BC的中点，又知厂房长
10米，为防雨，需在房顶铺满油毡。（每卷油毡宽1米，长10米）
如果你是该厂采购，需购买___ ____卷油毡。
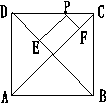
19、如图，四边形ABCD是边长为1的正方形，
P是ABCD的边CD上的任意一点，且PE⊥DB
于点E，PF⊥AC于点F，则PE+PF= 。
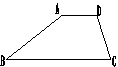20、如图，在梯形ABCD中，AD∥BC，并且AB=8，AD=3，CD=6，并且∠B+
∠C=900，则梯形面积S梯形ABCD= 。
三、耐心做一做：(本大题共8题，共80分)
21、化简（每小题5分，共20分）
（1）（2－
）
（2）（+2）（-2）
（3）
（4） 
22、（本小题8分）作出图中字母“H”先向右平移3格，再把平移所得的图案绕它的左下角的顶点顺时针旋转900的图
 |
23、（本小题8分）如图，是利用四边形的不稳定性制作的凉衣架。已知其中每个菱形的边长为20㎝，在墙上悬挂凉衣架的两个铁钉A、B之间的距离为
㎝，求∠1
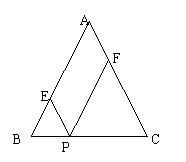24、（本小题8分）小明和小东经常在一块等腰三角形的草坪上玩耍，一天他们发现了一个有趣的现象：如图的草坪是等腰△ABC，AB＝AC，他们两人同在BC边上一点P，然后小明沿AC平行线PE(点E在AB上)、EA走向A处，小东沿BA的平行线PF(F点在AC上)、FA走向A处，当他两个步行速度一样时，他们同时到达A点，并且在BC边上不断改变P点位置。在步行速度一定时，到达A处的时间也完全一样，你知道为什么吗? 说说你理由。
25、（本小题8分）农村家庭打地基时，不像城市房基有专门仪器测量，他们往往采用土方法，先用绳子拉成四边形分别量出房基的长a和宽b（如图）。如果测得AD＝BC，AB＝CD，能保证房基是矩形吗？请你用学过的知识说明。如果不能保证是矩形，请说明还需要什么工序才能保证房基是矩形？（说出两种方法）
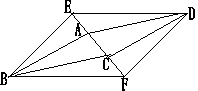
26、（本小题10分）已知：如图，在四边形ABCD中，AB=CD，BC=AD，E、F是对角线AC上的两点，且AE=CF。试说明BE=DF。
 |
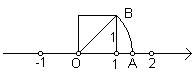
27、（本小题8分）我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x 轴于点A”，请根据图形回答下列问题：
（1）线段OA的长度是多少？（要求写出求解过程）
（2）这个图形的目的是为了说明什么？
（3）这种研究和解决问题的方式，体现了 的数学思想方法。
（将下列符合的选项序号填在横线上）
A． 数形结合 B. 代入 C. 换元 D. 归纳
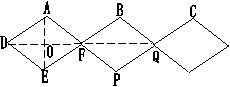
8、（本小题10分）如图1，图2，四边形ABCD是正方形，M是AB延长线上一点．直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F．
（1）如图1，当点E在AB边的中点位置时：
①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是 ；
②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是 ；
③请说明你的上述两个猜想的正确性。
（2）如图2，当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。
答案
一、1、A 2、B 3、C 4、B 5、C 6、B 7、C 8、D 9、C 10、A
二、11、
12、±6；-
;2，0 13、
14、C; 
;BCD 15、2006 16、4 17、 对角线相等（只填一个则可） 18、7 19、
20、
21、解：(1)原式=
-----------------------------1分
=12+2-4
-----------------------------------------------4分
=14-4-------------------------------------------------5分
(2)原式=
--------------------------------------------2分
=3-4-------------------------------------------------4分
=-1--------------------------------------------------5分
(3)原式=
--------------------------------------------2分
=
--------------------------------------------------4分
=1-----------------------------------------------------5分
(4) 原式=
+-------------------------------2分
=
-----------------------------------------------5分
22、解：连结DQ，AE
由图知DQ=2AB=
，则DF=
------------------------------2分
∵四边形ADEF是菱形
∴AE⊥DF，DO=OF，AO=OE--------4分
则DO=
在Rt△ADO中，∠ADO=900，AD=20㎝，DO=
根据勾股定理得：AO=
=10㎝---------------6分
∴AE=2AO=20㎝
∴AD=DE=AE
∴△ADE是等边三角形
∴∠1=600----------------------------------------------8分
23、解：画图略
平移正确--------------------4分；旋转正确-----------------------8分
24、解:∵PE∥ACPF∥AB ∴四边形AEPF是平行四边形--------4分
∴PE＝AF PF＝AE-------------------------------------------8分
∵小明和小东的速度相等
∴小明和小东会同时到达点A----------------------------------10分
25、解：不能保证四边形ABCD是矩形---------------------------------2分
∵AD=BC，AB＝CD∴四边形ABCD是平行四边形--------------4分
方法1：AC＝BD(对角线相等的平行四边形是矩形)-----------------7分
方法2：∠A＝900 (有一个角是直角的平行四边形是矩形---------10分
26、
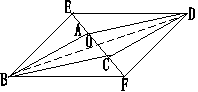
解：连结BD,设AC与BD相交于O
∵AB=CD BC=AD
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)--------------------------------------------------3分
∴OA=OC ，OB=OD(平行四边形的对角线互相平分)------5分
∵AE=CF
∴OE=OF------------------------------------------6分
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)--------------------------------------------------8分
∴BE=DF(平行四边形的对边相等)--------------------10分
27、(1)解：∵
=2--------------------------------------------1分
∴OB=
∴OA=OB=----------------------------------------------2分
(2)解：数轴上的点和实数一一对应关系------------------------------4分
(3)解：A---------------------------------------------------------6分
28、（1）①DE＝EF-----------------------------------------------------1分
②NE=BF------------------------------------------------------2分
③解：∵四边形ABCD是正方形∴AD＝AB，∠DAE＝∠CBM＝900
∵点N、E分别为AD、AB的中点∴DN＝
AD，AE＝AB
∴DN＝EB------------------------------------------------3分
在
中，∠ANE＝∠AEN＝450∴∠DNE＝1350
∵BF平分∠CBM∴∠FBM＝450∴∠EBF＝1350
∴∠DNE＝∠EBF-------------------------------------------4分
∵∠FBM＋∠DEA＝900 ∠ADE＋∠DEA＝900
∴∠FBM＝∠ADE--------------------------------------------5分
∴△DNE≌△EBF∴DE＝EF NE＝BF------------------------6分
(2)在AD上截取AN＝AE，连结NE，证法同上类似---------------10分