初二数学上册期末调研考试

　　　　　　　 八年级数学上册期末调研考试试题

 

题号	一	二	三				四	五	总分
			17	18	19	20
分数

一、单项选择题（每小题3 分，共30分）

1．下列运算正确的是（　　　）

（A） （B）　（C）（D）

2、下列艺术汉字中，不是轴对称的是(　　  )

　　　  奇　中　王　喜

（A）　　　　　 （B）　　　　  （C）　　　　　 （D）

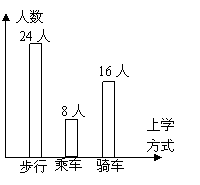3、一颗人造地球卫星的速度为2.88×10⁷米/时，一架喷气式飞机的速度为1.8×10⁶

则这颗人造地球卫星的速度是这架喷气式飞机的速度的（　　）

（A）1600倍　 （B）160倍　 （C）16倍　　（D）1.6倍

4、如图为雷锋中学八年级（2）班就上学方式作出调查后绘制

的条形图，那么该班步行上学的同学比骑车上学的同学（　　）

（A）少8人　 （B）多8人　（C）少16人　 （D）多16人

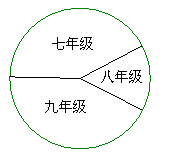
5、某校三个年级人数占全校人数的扇形统计图如图所示，

则八年级所在的扇形的圆心角的度数是（　 ）

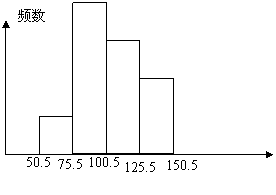（A）30^o（B）45^o（C） 60^o（D）72^o

6、如图是某班40名学生一分钟跳绳

测试成绩（次数为整数）的频数分布

直方图，从左起第一、二、三、四个

小长方形的高的比为1： 4 ：3 ：2，

那么该班一分钟跳绳次数在100次以

上的学生有（　　）

（A）6人 （B）8人

（C）16人（D）20人

7．在△ABC和△A₁B₁C₁中，下面给出

了四组条件，其中不一定能判定△ABC≌△A₁B₁C₁是（　　　）

（A）AB=A₁B₁, BC=B₁C₁, CA=C₁A₁

（B）∠C=∠C=90, AB=A₁B₁, BC=B₁C₁

（C）AB=A₁B₁, , CA=C₁A_1,∠B=∠B₁

（D）AB=A₁B₁, , CA=C₁A_1,∠A==∠A₁

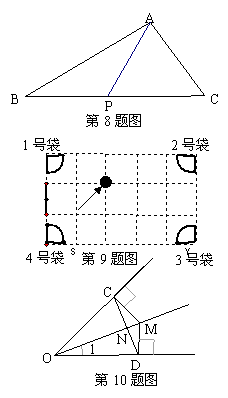
8．如图，P是△ABC的BC边上的一点，且BP=PA=AC=PC,

则∠B的度数为（　　　）

（A）20^O　 (B)30^O　 (C)40^O　 (D)50^O

9.如图是一个改造后的台球桌的平面示意图（虚线为正方形网格），图中四个角上的阴影分别表

四示个入球孔，如果一个球按图中所示的方向被

击出（球可以经过多次反弹），那么球最后落入

的球袋是（　　  ）

(A)1号袋 (B)2号袋 (C)3号袋 (D)4号袋

10．如图，点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，连接CD交OM于点N,则

下列结论：

①　　 MC=MD,②∠CMO=∠DMO,③OM⊥CD,且NC=ND,

④若∠1＝30⁰，则OD=2MD,正确的有（　　　 ）

（A）①②③　（B）①②④ （C）③④（D）①③④

二、填空题（每小题3分，共18分）

11．写出一个函数值随自变量的增大而减小的正比例函数

　　　　　　　　　  （写一个即可）

12．计算　　　　　　　　　　  。

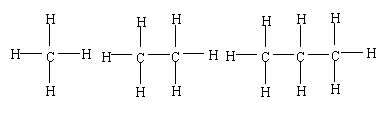
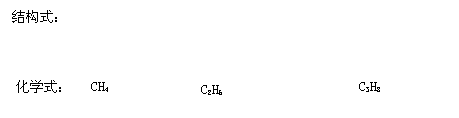
13．下列是三种化合物的结构式与化学式，则按其规律第4个化合物的化学式为　　　　。

14．分解因式：　　　　　　　   。

15．如图，△ABC与△ADC中，∠B=∠D=90^O,

要使△ABC≌△ADC，还需添加的一个条件是

　　　　　　　　　　 （写一个即可）。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

16．如图，正方形ABCD的边长为3，点E在AB上，

点F在BC的延长线上，且AE=AF,则四边形EBFD

的面积为：　　　　 。

三、解答与证明题（本题共4个小题，共32分）

17．（8分）求代数式的值，其中

18．（8分）如图，点C、E、B、F在一条直线上，AB⊥CF于B,DE⊥CF于E,AC=DF,

AB=DE。

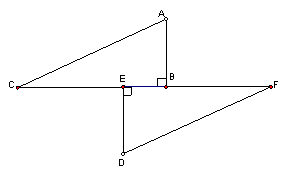求证CE=CF。

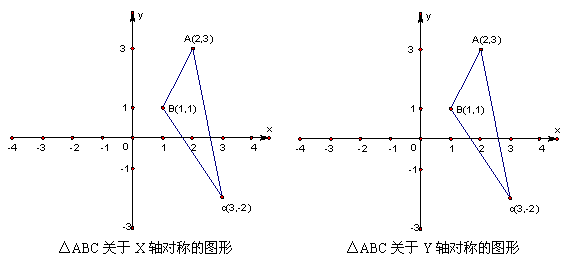19.(8分)如图，利用关于坐标轴对称的点的坐标特点，分别作出△ABC关于x轴和y轴对称的图形。

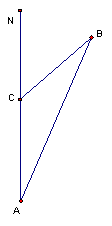
20.(8分)如图，一船上午9时从海岛A出发，以20海里/时的速度向正北方向航行，11时到达B处，从A 、B两处分别望灯塔C,测得∠NAC=32^O,∠NBC=64^O,求从B处到灯塔C的距离。

四、综合题（本题10分）

21．已知一次函数y=kx+b的图象经过点（1，1），且k、b满足k-b=-5.

(1)试确定该函数的解析式。（5分）

（2）若该函数的图象与y轴交于点A,则在该函数图象上是否存在点P,使PA=PO,若存在，请求出P点的坐标；若不存在，请说明理由。（5分）

五、综合题（本题10分）

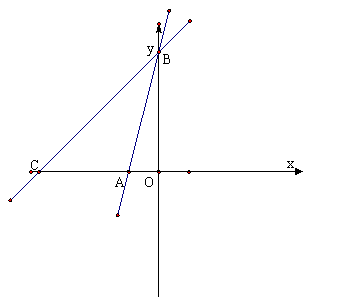22．如图，在直角坐标系xOy中，直线y=kx+b交x轴正半轴于A(-1,0),交y轴正半轴于B,C是x轴负半轴上一点，且CA=CO,△ABC的面积为6。

（1）求C点的坐标。（3分）

（2）求直线AB的解析式（3分）

 

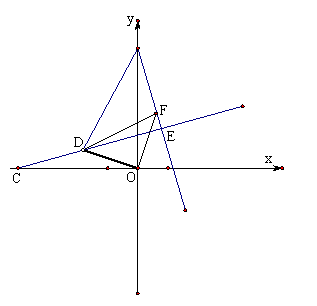（3）D是第二象限内一动点，且OD⊥BD,直线BE垂直射线CD于额，OF⊥CD交直线BE 于F .当线段OD,BD的长度发生改变时，∠BDF的大小是否发生改变？若改变，请说明理由；若不　　变，请证明并求出其值。（4分）

八年级数学参考答案及评分标准

一、单项选择题（每小题3 分，共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	A	C	B	D	D	D	C	B	B

二、填空题（每小题3分，共18分）

题号	11	12	13	14	15	16
答案	答案不唯一	4x6y2	C4H10	(p+2)(p-2)	答案不唯一	9

三、解答与证明题（本题共4个小题，共32分）

17．　　　　　　　　　　   ……2分

＝（x²+2xy+y²－x²+2xy—y²+4x²y²）÷4xy　　　　　　　　　   ……4分

=(4xy+4x²y²)÷4xy

=1+xy　　　　　　　　　　　　　　　　　　　　　　　　　  ……6分

∵ x=（），y=2

∴原式＝1+xy=1+1×2=3　　　　　　　　　　　　　　　　　  ……8分

18．证明：∵AB⊥CD,DE⊥CF

　　　　  ∴∠ABC=∠DEF=90^O　　　　　　　　　　　　　　  ……2分

　　　　 在Rt△ABC和Rt△DEF中，

　　　　

　　　　  ∴Rt△ABC≌Rt△DEF(HL)　　　　　　　　　　　　  ……6分

　　　　  ∴ BC=EF

　　　　  ∴BC—BE=EF—BE

　　　　  即：CE=BF　　　　　　　　　　　　　　　　　　　 ……8分

19．略。评分说明：每画对一个对称图形给4分。

20．解：∵ ∠NAC=32^O,NBC=64^O

 ∴∠C=∠NBC—∠NAC=64^O－32^O=32^O　　　　　　　　　  ……2分

∴∠C=∠NAC=32^O

∴BC=AC　　　　　　　　　　　　　　　　　　　　　 ……6分

∵AB=20×(11－9)＝40（海里）　　　　　　　　　　  ……7分

　　　 ∴BC=AC=40（海里）

答：B处到灯塔C处的距离为40海里。　 　　　　　　……8分

四、综合题（本题10分）

21．解: （1） ∵一次函数y=kx+b的图象经过点（1，1）　　……1分　

　　　∴k+b=1

　　　 　　　　　　　　　　　　 ……4分

　　 该函数的解析式为y=-2x+3.　　　　　　　　　　　　　  ……5分

　　　 （2）该函数的图象上存在一点P(0.75,　1.5),满足PA=PC.

该函数的解析式为y=-2x+3,当x=0时，y=3,

故点A的坐标为（0，3）　　　　　　　　　　　　　　　　　　  ……6分

∵PA=PO

∵点P在AO的垂直平分线上，

故点P的纵坐标为Y_P=1.5　　　　　　　　　　　　　　　　　　 ……8分

当Y_P=1.5时，

-2x_p+3=1.5

解得x_p=0.75　　　　　　　　　　　　　　　　　　　　　　　 ……9分

故点P的坐标为（0.75，1.5）　　　 　　　　　　　　　　　　……10分

五、综合题（本题10分）

22．（1）解：∵A(-1,0), ∴OA=1　　　　　　　　　　　　　　 ……1分

　　　　  又CA=CO, ∴(CA+AO)=CA可得CA=3　　　　　　 ……2分

　　　　 ∴CO=4,　　∴C(-4,0)　　　　　　　　　　　　　　  ……3分

(2)解：∵×BO=6,　　 ∴BO=4　　　　∴B(0,4)　　　 ……4分

　　　 又A(-1,0),用待定系数法可得直线AB的解析式为：y=4x+4　 ……6分

(3)解：当线段OD,BD的长度发生改变时，∠BDF的大小不变。

　 证明：可证△COD≌△BOF　　　　　　　　　　　　　　  ……8分

　　　∴OD=OF,又OD⊥OF

　　　 ∴∠ODF=45⁰

　　　 ∵OD ⊥ BD, ∴∠BDO=90^O,

　　　 ∴∠BDF=45^O

 即线段OD,BD的长度发生改变时，∠BDF的大小恒为45^o .　　　……10分