不等式的解集
例1.选择题
(1)若不等式(a+1)x>(a+1)的解集是x<1,那么必须满足 [ ]
(A)a<0 (B)a≤1
(C)a>-1 (D)a<-1
(2)若不等式(3a-2)x+2<3的解集是x<2,那么必须满足 [ ]
![]()
![]()
![]() [ ]
[ ]
![]()
![]()
分析:解答(1)、(2)两个小题的依据是不等式解的定义及不等式的性质.思维过程是:将一元一次不等式化为Ax>B(或Ax<B)形式后,再与已知的解的形式(如(1)中的x<1,(2)中的x<2)进行对照.重点注意的是不等号方向上的变化情况,从而依据不等式性质便可决定出x的系数A应为正数还是负数.还需注意计算数值,以便确定不等式两边同除以何值,由此再进一步确定出a应满足的条件.第(3)小题可用特殊值法来选择答案,因为结论是唯一正确的,所以只要在0<x<1中任意选择一个较易计算x2、1/x的值,分别求出1/x,x2与x再进行比较,便一目了然了.这种特殊值法在确定几个字母表示的数值之间大小关系时,常常起着简单、快捷的作用.
解:(1)∵x<1是不等式(a+1)x>a+1的解,依不等式性质3有a+1<0.
∴a<-1,选(D).
(2)∵(3a-2)x+2<3
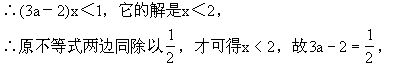
![]()
![]()
例2.解答题
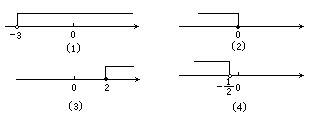
在数轴上表示下列不等式的解集
![]()
分析:首先画出数轴;其次在数轴上找准相应数字的位置:如本例中4个小题的-3,0,2,-1/2;第三确定好画实心圆点还是空心圆点,如(2)(3)应画实心圆点,而(1)(4)应画空心圆点.
解:如图
例3 填空题
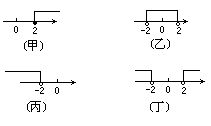
在括号中标明以上(甲)(乙)(丙)(丁)四图中分别表示(A)(B)(C)(D)哪种意义?
(A)小于-2或大于2的所有有理数
(B)大于-2且小于2的所有有理数
(C)不小于2的所有有理数
(D)小于-2的所有有理数
(甲)( );(乙)( );(丙)( );(丁)( ).
解:(甲)(C);(乙)(B);(丙)(D);(丁)(A).
说明:(甲)中表示的是大于或等于2的所有有理数,也就是不小于2的所有有理数,选(C);
(乙)中表示的是在-2和+2之间的所有有理数,也就是大于-2且小于2的所有有理数,选(B);
(丙)中表示的小于-2的所有有理数,选(D);
(丁)中表示数轴上在-2左边和+2右边部分,也就是小于-2或大于2的所有有理数,选(A).