10月27日 矩形、正方形(2)
快速反应
1. ____________________的矩形叫做正方形。
2. 正方形具有_________、___________、____________的一切性质。
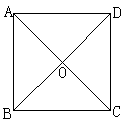
3. 如图,四边形ABCD是正方形,两条对角线相交于点O,OA=2,则∠AOB=________,∠OAB=________,BD =____________,AB=__________.
4. 第三题图中等腰三角形的个数是( )
A.4个 B.5个 C.6个 D.8个
5. 判断。
(1) 正方形一定是矩形。( )
(2) 正方形一定是菱形。( )
(3) 菱形一定是正方形。( )
(4) 矩形一定是正方形。( )
(5) 正方形、矩形、菱形都是平行四边形。( )
自主学习
1. 在下列性质中,平行四边形具有的是__________,矩形具有的是_________,菱形具有的是__________,正方形具有的是____________。
(1) 四边都相等;
(2) 对角线互相平分;
(3) 对角线相等;
(4) 对角线互相垂直;
(5) 四个角都是直角;
(6) 每条对角线平分一组对角;
(7) 对边相等且平行;
(8) 有两条对称轴。
2. 正方形两条对角线的和为8cm,它的面积为____________.
3. 在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到_____________
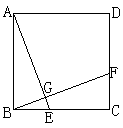
4. 如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1) AE与BF相等吗?为什么?
(2) AE与BF是否垂直?说明你的理由。
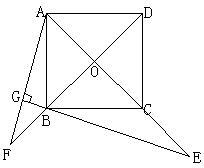
5. 如图,正方形ABCD中对角线AC、BD相交于O,E为AC上一点,AG⊥EB交EB于G,AG交BD于F。
(1) 说明OE=OF的道理;
(2) 在(1)中,若E为AC延长线上,AG⊥EB交EB的延长线于G,AG、BD的延长线交于F,其他条件不变,如图2,则结论:“OE=OF”还成立吗?请说明理由。
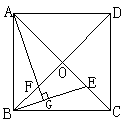
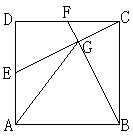
6. 如图,在正方形ABCD中,取AD、CD边的中点E、F,连接CE、BF交于点G,连接AG。试判断AG与AB是否相等,并说明道理。
正方形(
进一步理解正方形的判定方法,可研究以下几个问题:
(1)对角线相等的菱形是正方形吗?
(2)对角线互相垂直的矩形是正方形吗?
(3)对角线互相垂直且相等的四边形是正方形吗?若不是,还需增加什么条件?
(4)能说“四条便都相等的四边形是正方形吗?”
(5)四个角都相等的四边形是正方形吗?
[例1] 如图,四边形ABCD是正方形,两条对角线相交于点O,求∠AOB、∠OAB的度数.
[例2]
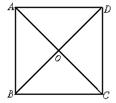
2.上右图中,有多少个等腰直角三角形?
答:以正方形的四个顶点为直角顶点,共有四个等腰直角三角形,以正方形两条对角线的交点为顶点的等腰直角三角形也有四个,因而共有八个等腰直角三角形.
(二)试一试 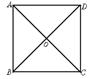
1.如何设计花坛?
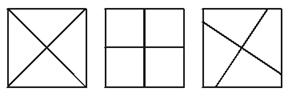
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
(图形如P102的图)
解:过正方形两条对角线的交点任意作两条互相垂直的直线,即可将正方形分成大小、形状完全相同的四部分.下面是其中的三种分法.