八年级(下)数学同步辅导
第四章 相似图形(§3~§7)
Ⅰ.梳理知识
1.相似多边形
(1)相似多边形的定义：①从图形上讲：一般而言，形状 的图形称为相识图形.②从边、角上讲：对应角 ，对应边 的两个多项式叫做相似图形.相似多边形 叫做相似比.③相似多边形的记法.
(2)相似多边形的性质：相似多边形的对应角 ，对应边 .
2.相似三角形
(1)相似三角形的定义：对应角 ，对应边 的两个三角形叫做相似三角形.相似三角形 叫做相似比.
(2)相似三角形的性质：相似三角形的对应角 ，对应边 .
(3)三角形相似的条件：
① ；② ；③ .
Ⅱ.典例剖析
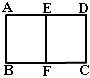例1.(1)E、F分别是矩形ABCD的边AD、BC的中点，若矩形ABCD矩形EABF，AB=1，求矩形ABCD的面积.
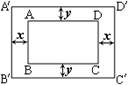(2)在一矩形ABCD的花坛与花坛四周修筑小路，使得相对两条小路的宽均相等.如果花坛AB=20米，AD=30米，试问小路的宽x与y的比值为多少时，能使使小路四周所围成的矩形A′B′C′D′与矩形ABCD相似？请说明理由.
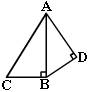例2.如图，ΔABC与ΔADB中，∠ABC=∠ADB=90°，AC=5cm，AB=4cm，如果图中的两个直角三角形相似，求AD的长.
例3.如图，D为ΔABC内一点，E为ΔABC外一点，且∠1=∠2，∠3=∠4.
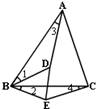(1)ΔABD与ΔCBE相似吗？请说明理由.
(2)ΔABC与ΔDBE相似吗？请说明理由.
例4.如图，点C、D在线段AB上，且ΔPCD是等边三角形.
(1)当AC，CD，DB满足怎样的关系时，ΔACP∽ΔPCB；
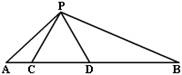(2)当ΔPCB∽ΔACP时，试求∠APB的度数.
Ⅲ.同步测试
一、选择题(每小题3分，共30分)
1.已知
，则
的值为（ ）
(A)
(B)
(C)3 (D)-3
2.在比例尺为1∶20的图纸上画出的某个零件的长是32mm，这个零件的实际长是（ ）
(A)64m (B)64dm (C)64cm (D)64mm
3.已知C是线段AB的黄金分割点(AC＞BC）, 则AC∶BC = ( )
(A)(
－1)∶2 (B)（ +1）∶2 (C)（3－）∶2 (D)（3+）∶2
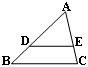
4.如图，E是平行四边形ABCD的边BC的延长线上的一点，连结AE交CD于F，则图中共有相似三角形（ ）
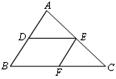
(A)1对 (B)2对 (C)3对 (D)4对
 |  |
(第4题图) (第5题图) (第6题图) (第 7题图)
5.ΔABC中，DE∥BC，且AD∶DB=2∶1，那么DE∶BC等于（ ）
(A)2∶1 (B)1∶2 (C)2∶3 (D)3∶2
6.如图，P是RtΔABC的斜边BC上异于B、C的一点，过点P做直线截ΔABC，使截得的三角形与ΔABC相似，满足这样条件的直线共有（ ）
(A)1条 (B)2条 (C)3条 (D)4条
7.如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（ ）
(A)
(B)
(C)
(D)
8.如图，ΔABC中，P为AB上一点，在下列四个条件中：①∠APC=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足ΔAPC与ΔACB相似的条件是（ ）
(A)①②③ (B)①③④ (C)②③④ (D)①②④
9.如图，ΔADE绕正方形ABCD的顶点A顺时针旋转90°，得ΔABF，连结EF交AB于H，则下列结论错误的是（ ）
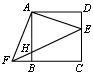(A)AE⊥AF (B)EF∶AF=
∶1 (C)AF2=FH•FE (D)FB∶FC=HB∶EC
 | |||
 | |||
(第8题图) (第9题图) (第10题图)
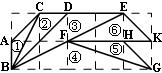
10.如图，在正方形网格上有6个斜三角形：①ΔABC，②ΔBCD，③ΔBDE，④ΔBFG，⑤ΔFGH，⑥ΔEFK.其中②～⑥中，与三角形①相似的是（ ）
(A)②③④ (B)③④⑤ (C)④⑤⑥ (D)②③⑥
二、填空题(每小题3分，共15分)
11.已知两数4和8，试写出第三个数，使这三个数中，其中一个数是其余两数的比例中项，第三个数是 (只需写出一个即可).
12.已知D、E分别是ΔABC的边AB、AC上的点，请你添加一个条件，使ΔABC与ΔAED相似.你添加的条件是 (只需添加一个你认为适当的条件即可).
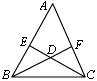
13.如图，锐角三角形ABC的边AB、AC上的高线CE和BF相交于点D，请写出图中的两对相似三角形： (用相似符号连接).
14.下列说法：①所有的等腰三角形都相似；②所有的等边三角形都相似；③所有等腰直角三角形都相似；④所有的直角三角形都相似.其中正确的是 (把你认为正确的说法的序号都填上).
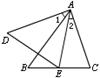
15.如图，已知∠1=∠2，若再增加一个条件就能使结论“AB•ED=AD•BC”成立，则这个条件可以是
.
 | |||
 | |||
(第13题图) (第15题图) (第17题图)
三、(每小题5分，共10分) (第16题图)
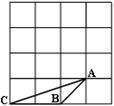
16.在方格纸中，每个小格的顶点叫做格点.以格点连线为边的三角形叫做格点三角形.如图，请你在4×4的方格纸中，画一个格点三角形A1B1C1，使ΔA1B1C1与格点三角形ABC相似(相似比不为1).
17.请设计三种不同的分法，将如图所示的直角三角形分割成四个小三角形，使得每个小三角形与原三角形都相似(要求画出分割线段，标出能够说明分法的必要记号，不要求写出画法，不要求说明理由).
四、(每小题6分，共24分)
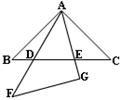18.将两块完全相同的等腰直角三角板摆放成如图所示的样子，假设图中的所有点、线都在同一平面内，回答下列问题：
(1)图中共有 个三角形.
(2)图中有相似(不包括全等)三角形吗？如果有，就把它们一一写出来.
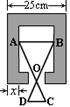19.已知零件的外径为25cm，要求它的厚度x ，需先求出它的内孔直径AB，现用一个交叉卡钳(AC和BD的长相等)去量(如图)，若OA∶OC=OB∶OD=3，CD=7cm.
求此零件的厚度x.
20.如图，在梯形ABCD中，AD⊥BC，∠BAD=90°，对角线BD⊥DC.
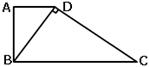(1)ΔABC与ΔDCB相似吗？请说明理由.
(2)如果AD=4，BC=9，求BD的长.
21.已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC， Q是CD的中点.
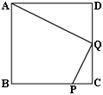ΔADQ与ΔQCP是否相似？为什么？
五、(每小题7分，共21分)
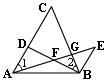22.已知：如图所示，D是AC上一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G，∠1=∠2.则BF是FG、EF的比例中项吗？请说明理由.
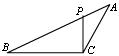
23.如图，CD是RtΔABC的斜边AB上的高，∠BAC的平分线分别交BC、CD于点E、F.
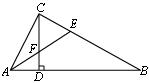AC•AE=AF•AB吗？说明理由.
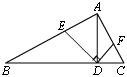24.如图，AD是RtΔABC斜边BC上的高，DE⊥DF，且DE和DF分别交AB、AC于E、F.则
吗？说说你的理由.