7．4 一次函数的图象（1）
一、填空题
1、一次函数y=kx+b（k≠0）的图象是 。
2、一次函数
的图象是一条经过（ ，0）、（0， ）的直线
3、已知一次函数y=3x＋4的图象过点（m，6）则m的值为
二、选择题
4、一次函数y=
的图象是（ ）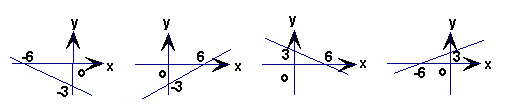
A B C D
5、下列各点中，一定在函数图象y=3x－1上的是（ ）
A、（
，1）
B、（
） C、（1，－1） D、（3，1）
6、直线y=kx经过点（3，－2），那么这条直线还通过点（ ）
A、（－2，3） B、（－3，2）
C、（2，3） D、（3，2）
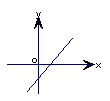
7、一次函数图象如图所示，则它的函数表达式为（ ）
A、y=－x+3 B、y=x+3
C、y=－x－3 D、y=x－3
8、已知一次函数图象经过点A（0，－2）和B（3，1）则这个函数表达式为（ ）
A、y=－x+2 B、y=x＋2 C、y=－x－2 D、y=x－2
三、解答题
9、已知一次函数图象经过点（0，2）和（1，－1）
（1）求这个一次函数的表达式
（2）在直角坐标中画出它的图象
（3）求此一次函数图象与坐标轴所围成的三角形面积
7.4 一次函数的图象（2）
一、填空题
1、在函数y=－6x中，y随x增大而 。
2、一次函数y=（k－2）x－1中，y随x增大而减少，则k取值范围是 。
3、在函数y=kx+b，k＞0，b＜0，则这个数图象不经过 象限。
二、选择题
4、当x＞0时，函数y=－2x图象在（ ）
A、第一象限 B、第二象限
C、第三象限 D、第四象限
5、点A(－5，y1)、B(－3，y2)都在直线y=
x上，则y1与y2关系是（ ）
A 、y1≤y2 B、y1=y2 C、y1＜y2 D、y1＞y2
6、函数y=－3x，y=
，y=6x共同点是（ ）
A、图象位于同样象限 B、y随x增大而减小
C、图象经过原点
D、y随x增大而增大
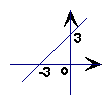
7、如图，直线
是一次函数y=kx+b的图象，其中k、b的取值范围是（ ）
A、K＞0，b＞0 B、k＞0，b＜0
C、k＜0，b＞0 D、k＜0，b＜0
8、直线y=2x－4与两坐标轴围成三角形面积是（ ）
A、16 B、8 C、6 D、4
三、解答题
9、已知正比例函数y=kx（k≠0）经过点（4，8）
（1）求c此函数解析式，并且画出图象
（2）说明y随x变化情况
（3）x为何值时，y＞6？
7.5 一次函数的简单应用（1）
一、填空题
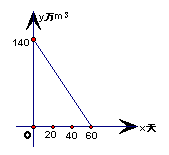1、由于连日无雨持续干旱，某水库存的蓄水量随时间的增加而减少，蓄水量y（万m3）与持续干旱的时间x（天）的关系如图，若水库蓄水量小于20（万m3）时为严重干旱
（1） 天不下雨，水库的蓄水量将减少到20（万m3）以下
（2） 天不下雨水库的水将干涸。
9、某商场搞促销活动,一次性购买x件T恤的售价为y元，x与y之间的关系如下表：
| x/件 | 1 | 2 | 3 | 4 |
| y/元 | 38 | 68 | 90 | 108 |
能将y看成一次函数吗？
7.5 一次函数的简单应用（2）
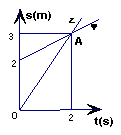2、甲、乙两物体沿同一直线同时同向匀速运动，如图表示他们运动路程S(m)与时间t（s）函数关系，根据图象回答：
（1）甲、乙两物体的初始位置 。
（2）甲速度 ，乙速度 。
（3）点A代表实际意义是 。
（4）写出甲乙两物体运动路程S与时间t关系式
。
10、随着科学手段不断更新，要求计算器进入课堂，某电子厂家经过市场调查，发现某种计算机器的供应量x1（万个）与价格y1（万元）之间的关系如图中供应线所示，而需求量x2（万个）与价格y2（万元）之间的关系如图中需求线所示，如图所示，回答下列问题：
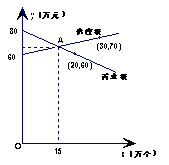（1）求y1与x1关系式及y2与x2关系式。
（2）如果你是这个电子厂的厂长，请你作出对生产及销售决策，使市场达到供需平衡。
一次函数测试卷
一、相信你一定能填对！
1．下列函数中，自变量x的取值范围是x≥2的是（ ）
A．y=
B．y=
C．y=
D．y=
·
2．下面哪个点在函数y=
x+1的图象上（ ）
A．（2，1） B．（-2，1） C．（2，0） D．（-2，0）
3．下列函数中，y是x的正比例函数的是（ ）
A．y=2x-1 B．y=
C．y=2x2 D．y=-2x+1
4．一次函数y=-5x+3的图象经过的象限是（ ）
A．一、二、三 B．二、三、四
C．一、二、四 D．一、三、四
5．若函数y=（2m+1）x2+（1-2m）x（m为常数）是正比例函数，则m的值为（ ）
A．m>
B．m=
C．m<
D．m=-
6．若一次函数y=（3-k）x-k的图象经过第二、三、四象限，则k的取值范围是（ ）
A．k>3 B．0<k≤3 C．0≤k<3 D．0<k<3
7．已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（ ）
A．y=-x-2 B．y=-x-6 C．y=-x+10 D．y=-x-1
二、你能填得又快又对吗？
8．已知自变量为x的函数y=mx+2-m是正比例函数，则m=________，该函数的解析式为_________．
9．若点（1，3）在正比例函数y=kx的图象上，则此函数的解析式为________．
10．已知一次函数y=kx+b的图象经过点A（1，3）和B（-1，-1），则此函数的解析式为_________
11．已知一次函数y=-3x+1的图象经过点（a，1）和点（-2，b），则a=________，b=______．
12．若一次函数y=kx+b交于y轴的负半轴，且y的值随x的增大而减少，则k____0，b______0．（填“>”、“<”或“＝”）
13．如果直线y=-2x+k与两坐标轴所围成的三角形面积是9，则k的值为_____．
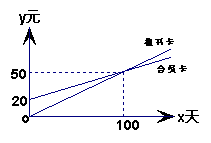
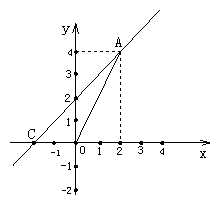14．如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，则此一次函数的解析式为__________，△AOC的面积为_________．
三、认真解答，一定要细心哟！
15．根据下列条件，确定函数关系式：
（1）y与x成正比，且当x=9时，y=16；
（2）y=kx+b的图象经过点（3，2）和点（-2，1）．
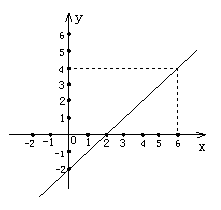
16．一次函数y=kx+b的图象如图所示：
（1）求出该一次函数的表达式；
（2）当x=10时，y的值是多少？
（3）当y=12时，x的值是多少？
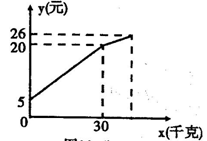
17．农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，结合图象回答下列问题：
（1）农民自带的零钱是多少？
（2）降价前他每千克土豆出售的价格是多少？
（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？
18．如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t（分钟）之间的函数关系的图象．（1）写出y与t之间的函数关系式．（2）通话2分钟应付通话费多少元？通话7分钟呢？
