7．4 一次函数的图象（1）
一、填空题
1、若一次函数y=kx－（2k+1）图象过原点，则函数解析式为 。
2、已知两个一次函数y=x+3k和y=2x－6的图象交点在y轴上，则k值为
。
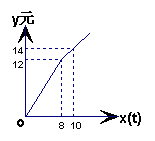3、某自来水公司中为了鼓励市民节约用水，采取分段收费标准，某户居民每月应交水费y（元）是用水量x（t）的函数，其图象如图所示
（1）与出x≤8时，函数表达式 。
（2）写出x＞8时，函数表达式 。
（3）由图象知收费标准为 。
（4）当某户居民该月用水15吨，则应交水费 元。
二、选择题
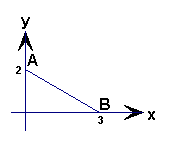
4、如图，线段AB的解析式为（ ）
A、
B、
C、（0≤x≤3）
D、
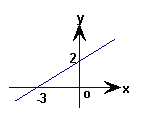
5、已知函数图象如图所示，
的x取值范围是（ ）
A、x＜0 B、x＞－3
C、x＜2 D、x＜－3
三、已知一次函数y=kx+b的图象经过点A（1，5），B（0，2）且与x轴相交于点C，求（1）这个一次函数的解析式（2）△ABO面积
7.4 一次函数的图象（2）
一、填空题
1、函数y=－6x（x≤0）图象是一条 线，y随x增大而 。
2、一次函数y=kx+b（k≠0）图象与x轴交点坐标是 ，与y轴交点坐标是
。
3、若直线y=kx+b经过点A（2，0），B（0，2），C（m，3）则m的值为 。
二、选择题
4、函数y=kx－5，k取不同的值，它的图象是（ ）
A、一条经过点（0，－5）的直线
B、一组互相平行的直线
C、一组相交于点（0，－5）的直线
D、一条与y轴的交点在x轴上方的直线
5、一次函数y=（3a－1）x+5图象上两点A（x1、y1），B（x2、y2）当x1＜x2时，y1＞y2，那么a取值范围是（ ）
A、a＞0
B、a＜0
C、a＞
D、a＜
三、已知y－1与x成正比例，当x=－2时，y=4
（1）求出y与x函数表达式
（2）把（1）中函数图象向上平移2个单位，设点（a，－2）在这个平移图象上求a值。
（3）如果x取值范围0≤x≤5，求y取值范围
7.5 一次函数的简单应用（1）
1、函数y=－x+4（－2≤x≤5）的图象与x轴的交点坐标是 ；函数的最大值是
2、对任意实数m，直线y=（3－m）x+2m经过一个定点，这个定点是 。
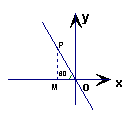3、如图，已知：直线l与x轴的夹角等于600，且过原点，这条直线l的函数解析式
。
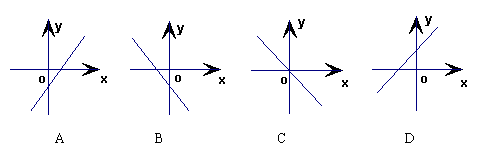
4、一次函数y=ax+b，ab＜0，则其大致图象正确的是（ ）
5、如果正比例函数y=kx（k≠0）的自变量取值增加1，函数y的值相应减少4，则k的值为（ ）
A、4 B、－4
C、
D、
6、为了保护学生视力，课桌椅的高度都是按一定的关系配套设计，研究表明：假设课桌的高度为ycm，椅子的高度为xcm（不含靠背）则y应是x的一次函数，下表列出两套符合条件的课桌椅的高度。
| 第一套 | 第二套 | |
| 椅子高度x（cm） | 40.0 | 37.0 |
| 桌子高度y（cm） | 75.0 | 70.2 |
(1)试确定y与x的函数表达式
(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌,它们是否配套?请通过计算说明理由.
7.5 一次函数的简单应用（2）
1、关于x的一次函数
的图象与y轴交于x轴下方，且y值随x的增大而减小，则a的范围是
。
2、已知点M（－3，m）是函数y=2x+1图象上一点，则点M到x轴的距离是（ ）
A、5
B、4
C、
D、5或3
3、如果一次函数自变量x的取值范围是－1＜x＜3，函数y的取值范围是－3＜y＜9，那此此函数的解析式为（ ）
A、y=3x B、y=－3x+6
C、y=－3x或y=3x－6 D、y=3x或y=－3x+6
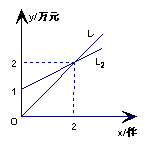4、如图，l1表示某机床公司一天的销售收入与机床销售量的关系，l2表示该公司一天的销售成本与机床销售量的关系。
（1）当x=1时，销售收入= 万元，销售成本= 万元。利润（收入－成本）= 万元。
（2）一天销售 件时，销售收入等于销售成本。
（3）l1对应的函数表达式是 。
（4）你能写出利润与销售量间的函数表达式吗？
一次函数综合测试
1、下列函数关系中表示一次函数的有（ ）①
②
③
④
⑤
A.1个 B.2个 C.3个 D.4个
2、下列函数中，图象经过原点的为( )
A．y=5x+1 B．y=-5x-1
C．y=-
D．y=
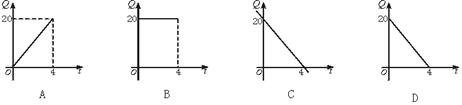
3、一水池蓄水20 m3，打开阀门后每小时流出5 m3，放水后池内剩下的水的立方数Q (m3)与放水时间t(时)的函数关系用图表示为( )
4、已知点（-4，y1），（2，y2）都在直线y= - x+b上，则y1 、y2大小关系是( )
（A）y1 >y2 （B）y1 =y2 （C）y1 <y2 （D）不能比较
5、每上5个台阶升高1米，升高米数h是台阶数S 的函数关系式是( )
A. h=5S B. h=S+5 C.h=
D.h=S-5
6、直线
,
,
共同具有的特征是 （ ）
A.经过原点
B.与
轴交于负半轴
C.随
增大而增大
D.随增大而减小
7、如果直线
经过一、二、四象限，则有（ ）
A . k>0,b>0 B. k>0,b<0 C. k<0,b>0 D.k<0,b<0
8、直线经过A(0,2)和B(3,0)两点,那么这个一次函数关系式是( )
(A)
(B)
(C)
(D)
9、下面哪个点不在函数
的图像上（ ）
A、（-5，13） B.（0.5，2） C（3，0） D（1，1）
10、已知函数
，当k 时，它是正比例函数，当k
时它是一次函数。
11、速度60千米/时的匀速运动中，路程S与时间t的关系
12、写出同时具备下列两个条件的一次函数表达式（写出一个即可） .
（1）y随着x的增大而减小。 （2）图象经过点（1，-3）
13、一次函数y= 8x+4的图象与x轴交点坐标是__________，与y轴交点坐标是___________。
14、已知一次函数当x=1时y=-2，当x=2时y=0
(1) 求这个一次函数；（3分）
(2)作出它的图象（2分）
（3）求出图象与两条坐标轴围成的三角形面积（3分）
15．已知直线l与直线y＝2x＋1的交点横坐标为2，与直线y＝－x－8的交点的纵坐标为－7，求直线l的解析式．
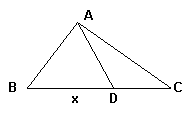
16、如图，△ABC边BC长是10，BC边上的高是6cm,D点在BC上运动，设BD长为x,请写出△ABD的面积y与x之间的函数关系式： __________，自变量x的取值范围是________，函数值y的取值范围是___________。
17．已知雅美服装厂现有A种布料70米，B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．
①求y（元）与x（套）的函数关系式，并求出自变量的取值范围；
②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？