§7.1 常量与变量
一、填空题：
1、在匀速运动公式S=Vt中，V表示速度，t表示时间，S表示在时间t内所走的路程，则变量是 ，常量是 。
2、某方程的两个未知数之间的关系为y=-3x2+5, 变量是 ，常量是 。
3、茶叶蛋每只0.3元，在买卖鸡蛋的过程中， 是常量， 是变量；设买茶叶蛋的个数为x（个），所付的钱数为y（元），它们的关系可表示为 。
二、选择题：
4、下列关系式中，变量x= - 1时，变量y=6的是（ ）
A y= 3x+3 B y= -3x+3 C y=3x – 3 D y= - 3x – 3
5、球的体积公式：V=
πr3,r表示球的半径，V表示球的体积。当r=3时，V=（ ）
A 4 π B 12π C 36π D π
6、在平整的路面上，某型号汽车紧急刹车后仍将滑行S米，一般地有经验公式S=V2/300，其中V表示刹车前汽车行驶的速度（单位：千米/小时），计算当V取80时，相应的S值约为（ ）
A 21米 B 21千米 C 30米 D 30千米
7、一个容量为100立方米的水池，原有水60立方米，现以每分钟2立方米的速度匀速向水池中注水，设注水时间t分钟，水池有水Q立方米，则注满水池的时间t为（ ）
A 50分钟 B 20分钟 C 30分钟 D 40分钟
8、平行四边形相邻两角中，其中一个角的度数y与另一个角的度数x 之间的关系是
A y =x B y= 90 – x C y= 180 – x D y= 180 + x
三、解答题：
某弹簧的自然长度为3cm，在弹性限度内，所挂物体的质量x每增加某1千克，弹簧长度y增加0.5厘米。则有关系式y=3+0.5x，指出其中的变量与常量。
§7.2 认识函数(1)
1、小明用30元钱去购买价格为每件5元的某种商品，求他剩余的钱y(元)与购买这种商品x件之间的关系 。当x=5时，函数值是 ，这一函数值的实际意义是 。
2、某商店售货时，在进货价的基础上加一定的利润，其数量x与售价y如下表示，根据表中所提供的信息，售价y与售货数量x的函数解析式为（ ）
| 数量x(千克 ) | 1 | 2 | 3 | 4 | ··· |
| 售价y(元) | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | ··· |
A y=8.4x B y= 8x +0.4 C y=0.4x +8 D y=8x
3、地壳的厚度约为8~40km，在地表以下不太深的地方，温度可按y=35x+t计算，其中x是深度，t是地球表面温度，y是所达深度的温度。当x为22km时，地壳的温度（地表温度为2°C）（ ）
A 24°C B 772°C C 70°C D570°C
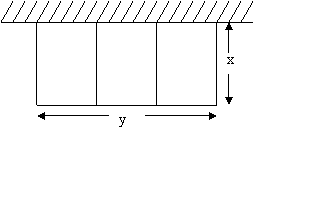
4、围猪舍三间，它们的形状是一排大小相等的三个矩形，一面利用旧墙，包括隔墙在内的其他各墙均用木料，已知现有木料可围24米的墙，设整个猪舍的长为x（米），宽为y（米），则y关系x的函数关系式为 。
 |
§7.2 认识函数(2)
1、
一个长方形的长比宽大3cm，如果宽是xcm，那么这个长方形的面积是 ，当x为8时，长方形的面积为 .
2、 函数 中，自变量x的取值范围 。
3、 已知正方形的边长为xcm，若把这个正方形的每边长都减少3cm，则正方形减少的面积为（ ）
A 3 B 6x – 9 C (x-3)2 D 6x
4、一台机器开始工作时油箱中储油4升，如果每小时耗油0.5升，那么油箱中所剩油y（升）与它工作时间t(小时)之间的函数关系式是
A y= 0.5 t B y= 4 - 0.5 t C y= 4+ 0.5 t D y= 4 / t
5、求下列函数自变量的取值范围。
（1）
（2）
7.3 一次函数(1)
1、一次函数
中一次项系数k值为
。
2、一个小球由静止开始在一个斜坡上向下滚动，其速度每秒增加3m，则小球速度V（m/s）时间t（s）之间关系式为 。
3、一次函数y=kx+2，当x=3时y=－7，则k的值是 。
4、下列说法正确的是（ ）
A、一次函数是正比例函数 B、正比例函数是一次函数
C、不是正比例函数就不是一次函数 D、正比例函数不是一次函数
5、下列关于x的函数中，是正比例函数的是（ ）
A、
B、
C、
D、
7.3 一次函数（2）
1、已知一次函数
，当x=1时，y=3，则b的值是
。
2、某汽车行驶时，油箱内装满汽油70升，如果每时耗油7升，油箱内剩余油量y（升）与时间x（时）之间的函数关系式为 。
3、已知y与x－1成正比例，且当x=－5时，y=3，写出y与x之间函数关系式
。
二、选择题
4、一次函数y=kx+3中，当x=2时，y的值为5，则k的值为（ ）
A、1 B、－1 C、5 D、－5
5、一次函数当x=0时，y=－2，当x=3时，y=1，那么这个函数的表达式是（ ）
A、
B、
C、
D、
第七章一次函数(7.1—7.3)综合试卷
一、填空题
1．在圆的周长和半径之间的关系式C=2πr中，C随着r的变化而变化．其中，_______是常量，_______是变量．
2．有一棵树苗，刚栽下去时树高1.2米，以后每年长高0.2米，设x年后树高为y米，那么y与x之间的函数解析式为_______。
3．当x=5时，函数y=+4的值是_______。
4．函数y=中，自变量x的取值范围是_______。
5．已知y与x成正比例，当X=-2时，y=6，那么比例系数k=_______。
6．已知一次函数y=-2x+b，当x=1时，y=2，那么b的值是_______。
7．已知y-2与x成正比例，并且当x=-1时，y=7，那么y与x之间的函数解析式是_______。
8．已知一次函数y=x+5，当y>1时，自变量x的取值范围是_______。
9．等腰三角形的周长为20cm，设腰长为xcm，底边长为ycm，那么y与x之间的函数解析式是_______，其中自变量x的取值范围是_______。
二、选择题
10．在某地，温度T(℃)与高度d(米)之间的关系可以近似地用T=10-来表示，那么，当高度d=900米时，温度T为 ( )
A．8℃ B．6℃ C．5℃ D．4℃
11．如果每盒圆珠笔有12支，售价18元，那么圆珠笔的售价y(元)与圆珠笔的支数x之间的函数关系式是 ( )
A．y=1．5x(x为自然数) B．y=x(x为自然数)
C．y=12x(x为自然数) D．y=18x(x为自然数)
12．正方体的棱长是a，表面积为S，那么S与a之间的函数解析式是( )
A．S=4a2 B．S=a3 C． S=6a2 D．S=8a2
13．一根蜡烛长20cm，点燃后每小时燃烧5cm，燃烧时剩下的高度h(cm)与燃烧时间t (小时)(0≤t≤4)之间的函数解析式是 ( )
A．h=4t B．h=5t C．h=20-4t D．h=20-5t
14．已知下列函数：①y=2x-1；②y=-x；③y=4x；④y=x/2。其中属于正比例函数的有( )
A．1个 B．2个 C．3个 D．4个
15．一次函数y=kx+b中，k为( )
A．非零实数 B．正实数 C．非负实数 D．任意实数
16、写出下列函数关系式，并判断其中哪些是正比例函数，哪些是一次函数。
（1）行驶200千米路程，车速V（千米/时）与行驶的时间t（小时）的关系。
（2）三角形底边上的高h一定，它的面积S与底边长a的关系。
（3）游泳池内有水15m3，现以每分钟3m3的流量往池里注水，80分钟可以将水池注满，池内水量Q（m3）与注水时t（分）之间关系
17．已知y与x成正比例，且x=2时，y=-6．求：
(1)y与x的函数关系式；
(2)当y=12时，x的值．
18．(6分)已知y是x的一次函数，当x=-2时，y=8；当x=-1时，y=5．求y与x的函数解析式。
19、已知y与x+2成正比例，且当x=1时，y=－6
（1）求y与x之间的函数关系式
（2）当y=2时，求自变量x值
20、平行四边形的周长为18cm，两条邻边不相等，其中较大的一条边长为ycm，较小的一条边长为xcm．求y与x之间的函数解析式，并写出自变量x的取值范围。