§7.1 常量与变量
1、一边固定为acm 的三角形面积S(cm2)与固定边上的高h（cm）之间的关系是S= 
ah , 变量是 常量是
。
2、用总长为80m的篱笆围成一个矩形场地，若矩形的面积和一边的长分别用y与x来表示，那么它们之间的关系式为y=x(40-x),在这个式子中，常量是 ,变量是 .
3、某同学在做电学实验时，记录下电压（伏特）与电流（安培）有如下对应关系：
| 电流 | 。。。 | 2 | 4 | 6 | 8 | 10 | 。。。 |
| 电压 | 。。。 | 15 | 12 | 9 | 6 | 3 | 。。。 |
请你估计，若电流是5安培时，电压为（ ）伏特。
A 10.5 B 6 C 80 D 18
4、三角形的一条边长为a，这条边上的高为h，h为常量，已知当a=6时，三角形面积S=12，则当a=4时，S的值为（ ）
A 4 B 6 C 8 D 10
5、扇形的面积公式：S=nπr2/360,其中r表示扇形的半径，n表示扇形圆心角的度数，S表示扇形的面积。（1）求半径为3，不同圆心角度数的扇形面积过程中，哪些是变量，哪些是常量。（2）半径为3，n分别取45，225，240，216时，求出相应的S的值。
10、如图，一个四棱柱的底面是一个边长为10cm的正方形，它的高变化时，棱柱的体积也随着变化。
（1） 指出问题中的变量与常量；
（2） 当高为7cm时，棱柱的体积；
（3） 棱柱的高由1cm变化到50cm时，它的体积由 变化成 。
§7.2 认识函数(1)
1、无线市话小灵通的通话收费标准为：前3分钟（不足3分钟按3分钟计）为0.2元，3分钟后每分钟收0.1元，则一次通话时间x分钟（x>3）与这次通话的费用y（元）之间的关系式为 。
2、把方程xy=3x-5y 改成用x的代数式表示y的函数形式为 ，当x=5时，y的值为 。
3、某中学要在校园内划出一块面积是100cm2的矩形土地做花圃，设这个矩形的相邻两边的长分别为xm和ym，那么y关于x的函数关系式可表示为（ ）.
A y=100x B y= 100 – x C y=50 – x D
4、一个正方形的周长p（cm）与这个正方形的面积S（cm2）之间的关系为（ ）。
 |  |
A S=4p2 B S= p2 C D
5、当x=2时，函数y=kx+10与函数y=3x+3k的值相等，则k的值为（ ）
A 2 B 4 C 6 D 8
§7.2 认识函数(2)
1、商家为了促销，常用打折的办法。一种商品原零售价为P元，先后两次打折，第一次打八折，第二次打七折，两次打折后的零售价为 元，比原来零售价便宜 元。
2、已知长方形的长是宽的3.3倍，如果宽为m，那么长方形的面积S为 .
3、一个长方形的周长为8cm ，若长是xcm，宽是ycm，则y关于x的函数关系式是 。
A y = 4 +x B y= 4 – x C y = 8+ x D y = 8/x
4、函数 中，自变量x的取值范围（ ）
A x≥-2 B x≥-10 C x≤-10 D x≤-5
5、用4x cm长的铁丝，围成一个长方形，要使长比宽多6cm，求围成的长方形的面积y与x的函数关系式。
7.3 一次函数(1)
1、某音像社对外出租光盘的收费方法是：每张光盘在租出后的头两天每天收0.8元，以后每天收0.5元，那么一张光盘在租出的第n天（n是大于2的自然数）应收租金＿＿＿＿元。
2、已知某种商品买入价为x元，销售价为y元，毛利率为45%（毛利率=
），则y关于x的函数解析式为
。
3、油箱有油40升，油从管道中匀速流出，100秒可流完，油箱中剩油量Q（升）与流出时间t（秒）间的函数关系式是（ ）
A、Q=40－
B、Q=40+
C、Q=40－
D、Q=
4、已知等腰三角形周长20cm，将底边长y（cm）表示成腰长x（cm）的函数关系式是y=20－2x，则自变量x取值范围是（ ）
A、0＜x＜10 B、5＜x＜10
C、一切实数 D、x＞0
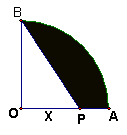10、如图，OB⊥OA于点O，以OA为半径画弧，交OB于B，点P是半径OA上的动点，已知OA=2cm，设OP=xcm，阴影部分的面积为ycm2
（1）求y与x之间的函数关系式；
（2）利用第（1）题结果，求以
为弓形的面积。
7.3 一次函数（2）
1、已知y=
，y是x的正比例函数，则m的值为
。
2、如果等腰三角形顶角为x度，底角为y度，则y关于x的函数关系式为
。
10、某人在银行的信用卡中存入2万元，每次取出50元，若卡内余钱为y（元），取钱的次数为x（利息忽略不计）
（1）写出y与x之间的函数关系式
（2）求自变量x的取值范围
（3）取多少次钱后，余额为原存款的
第七章一次函数(7.1—7.3)综合试卷
一、填空题
1．在圆的周长和半径之间的关系式C=2πr中，C随着r的变化而变化．其中，_______是常量，_______是变量．
2．有一棵树苗，刚栽下去时树高1.2米，以后每年长高0.2米，设x年后树高为y米，那么y与x之间的函数解析式为_______。
3．当x=5时，函数y=+4的值是_______。
4．函数y=中，自变量x的取值范围是_______。
5．已知y与x成正比例，当X=-2时，y=6，那么比例系数k=_______。
6．已知一次函数y=-2x+b，当x=1时，y=2，那么b的值是_______。
7．已知y-2与x成正比例，并且当x=-1时，y=7，那么y与x之间的函数解析式是_______。
8．已知一次函数y=x+5，当y>1时，自变量x的取值范围是_______。
9．等腰三角形的周长为20cm，设腰长为xcm，底边长为ycm，那么y与x之间的函数解析式是_______，其中自变量x的取值范围是_______。
二、选择题
10．在某地，温度T(℃)与高度d(米)之间的关系可以近似地用T=10-来表示，那么，当高度d=900米时，温度T为 ( )
A．8℃ B．6℃ C．5℃ D．4℃
11．如果每盒圆珠笔有12支，售价18元，那么圆珠笔的售价y(元)与圆珠笔的支数x之间的函数关系式是 ( )
A．y=1．5x(x为自然数) B．y=x(x为自然数)
C．y=12x(x为自然数) D．y=18x(x为自然数)
12．正方体的棱长是a，表面积为S，那么S与a之间的函数解析式是( )
A．S=4a2 B．S=a3 C． S=6a2 D．S=8a2
13．一根蜡烛长20cm，点燃后每小时燃烧5cm，燃烧时剩下的高度h(cm)与燃烧时间t (小时)(0≤t≤4)之间的函数解析式是 ( )
A．h=4t B．h=5t C．h=20-4t D．h=20-5t
14．已知下列函数：①y=2x-1；②y=-x；③y=4x；④y=x/2。其中属于正比例函数的有( )
A．1个 B．2个 C．3个 D．4个
15．一次函数y=kx+b中，k为( )
A．非零实数 B．正实数 C．非负实数 D．任意实数
16．已知y与x成正比例，且x=2时，y=-6．求：
(1)y与x的函数关系式；
(2)当y=12时，x的值．
17．已知y是x的一次函数，当x=-2时，y=8；当x=-1时，y=5．求y与x的函数解析式。
18．平行四边形的周长为18cm，两条邻边不相等，其中较大的一条边长为ycm，较小的一条边长为xcm．求y与x之间的函数解析式，并写出自变量x的取值范围。
19．(8分)如图，长方形ABCD中，AB=4，BC=8．点P在AB上运动，设PB=x，图中阴影部分的面积为y．
(1)写出阴影部分的面积y与x之间的函数解析式；
(2)点P在什么位置时，阴影部分的面积等于20?