暑假作业:直棱柱测试
班级: 姓名: 学号:
一、填空题:
1、由若干个 围成的几何体叫做多面体.
2、直棱柱的侧面都是 .直棱柱的相邻两条侧棱互相 .
3、观察一个物体时,把从正面看到的图形叫做 ,把主视图、俯视图、左视图合起来,就叫做 .
 4、画三视图必须遵循的法则是:
.
4、画三视图必须遵循的法则是:
.
5、长方体是 棱柱,它由个 面围成,有 条侧棱.
6、直六棱柱的其中一条侧棱长为5cm,那么它的所有侧棱长度之和为 cm.
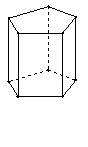
7.如图,这个几何体的名称是 ,它是由 个
 面, 条棱, 个顶点组成的.
面, 条棱, 个顶点组成的.
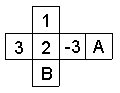
8.如图是一个正方体纸盒的展开图,其中的四个正方形内标有数字1,
2,3和-3.要在其余正方形内分别填上-1,-2,使得按虚线折成正
方形后,相对面上的两
| |
 9.一个几何体的三视图都是半径相同的圆,则这个几何体是 .
9.一个几何体的三视图都是半径相同的圆,则这个几何体是 .
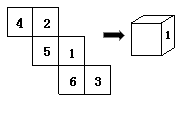
10.如图为一个正方体的表面展开图,现将它折叠成立
方体,则左侧面上标有的数字是 .
 11、主视图、左视图、俯视图都全等的几何体是
.
11、主视图、左视图、俯视图都全等的几何体是
.
12、棱柱分为 棱柱和 棱柱,
直棱柱的侧面是 .
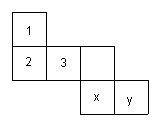
13、若要使如图表面展开图折叠成立方体后,
相对面上的两个数之和为6,则x= ,y= .
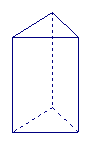
14、如图所示,正三棱柱底面边长是2cm,侧棱长为4cm,
侧面展开图的面积为 cm2
 15、直三棱柱有__ _条棱,__
_个顶点,_ __个面;直四棱柱有__
_条棱,__ _个顶点,_ ___个面; 则直n棱柱有___条棱,___个顶点,____ 个面;
15、直三棱柱有__ _条棱,__
_个顶点,_ __个面;直四棱柱有__
_条棱,__ _个顶点,_ ___个面; 则直n棱柱有___条棱,___个顶点,____ 个面;
同一个直棱柱的点、面、棱有什么数量关系?
。
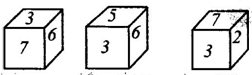
 16、一个正方体的6个面分别标有“2”, “3”,
16、一个正方体的6个面分别标有“2”, “3”,
“4”,“5”,“6”,“7”其中一个数字,右图表示的是正方体3种不同摆法,当“3”在上面时下面的数字是____。
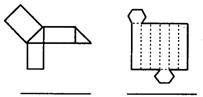
17.如图,请你在横线上写出哪种立体图形的表面能展开成下面的图形;
18.2个完全相同的长方体的长、宽、高分别为5cm、4cm、3cm,把它们叠放在一起组成一个新长方体,在这个新长方体中,体积是 cm3,最大表面积是_ cm2;
 二、选择题:
二、选择题:
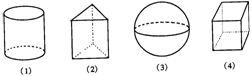
1、下面几何图形中,是直棱柱体的是( )
A.(1)(2) B.(1)(3)
 C.(2)(3) D.(2)(4)
C.(2)(3) D.(2)(4)
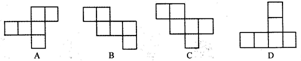
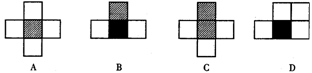
2、下列图形中,不可能围成正方体的是( )
 3、如图几何体的主视图是
( )
3、如图几何体的主视图是
( )

4、下列几何体中,不属于多面体的是( )
A.正方体 B.三棱柱 C.长方体 D.圆柱
5、分析下列说法: ①长方体、正方体都是棱柱 ;②三棱柱的侧面是三角形;③圆锥的三视图中:主视图、左视图是三角形,俯视图是圆; ④球体的三种视图均为同样大小的图形;⑤ 直六棱柱有六个侧面、侧面为长方形.其中正确的说法有( )种
A.2 B.3 C.4 D.5
6、一个直棱柱有12个顶点,那么它的面的个数是( )
A.10个 B.9个 C.8个 D.7个
7、下列说法中正确的是( )
A.直四棱柱是四面体 B.直棱柱的侧棱长度不一定相等
C.直五棱柱有5个侧面 D.正方体是直四棱柱,长方体不是直四棱柱
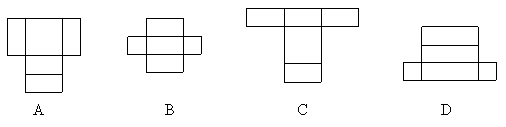
8.下列各图中,不是直四棱柱的表面展开图的是( )

 9、下列各图中,不可能折成无盖的长方体的是( )
9、下列各图中,不可能折成无盖的长方体的是( )
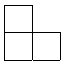
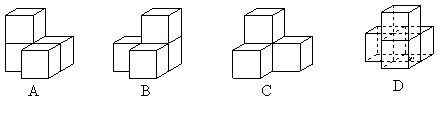 10、.由四个大小相同的小正方体搭成的几何体的左视图如图所示,则这个几何体的搭法不能是( )
10、.由四个大小相同的小正方体搭成的几何体的左视图如图所示,则这个几何体的搭法不能是( )
 |
11、图(1)是一个水平摆放的小正方体木块,图(2)、(3)
是由这样的小正方体木块叠放而成,按照这样规律继续叠放
下去,至第七个叠放图形中,小正方体木块总数应是( )
A.25 B.66 C.91 D.120
 12、如果用□表示1个立方体,用
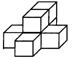
12、如果用□表示1个立方体,用![]() 表示两个立方体叠加,用■表示三个立方体叠加,那么下图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
表示两个立方体叠加,用■表示三个立方体叠加,那么下图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
 | |||
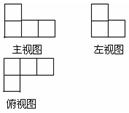 | |||
13. 如图是由一些相同的小正方体构成的几何体的三视图,则这些相同的
小正方体的个数是 ( )
A.4个 B.5个 C.6个 D.7个
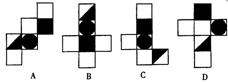
![]() 14、 如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是( )
14、 如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是( )
![]()
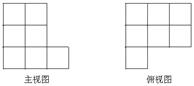
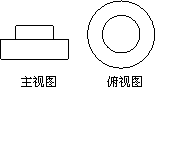
![]() 15、一个直六棱柱的主视图和俯视图如右图所示,则它的左视图是( )
15、一个直六棱柱的主视图和俯视图如右图所示,则它的左视图是( )
A B C D
 16、小明掷骰子游戏,连续四次掷出的结果如图所示,请问第四次掷出的结果中
16、小明掷骰子游戏,连续四次掷出的结果如图所示,请问第四次掷出的结果中
 底面上的数字是
( )
底面上的数字是
( )
 17.棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积是( )
17.棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积是( )
A.36cm2 B.33cm2 C.30cm2 D.27cm2
18 、一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的
主视图与俯视图如图所示,根据小明画的视图,请你猜礼物是( )
 A.钢笔 B.生日蛋糕 C.光盘 D.一套衣服
A.钢笔 B.生日蛋糕 C.光盘 D.一套衣服
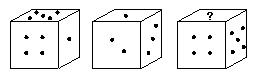
19、如图一枚骰子抛掷三次,得三种不同的结果,
则写有“?”一面上的点数是( )
A.1 B.2 C.3 D.6
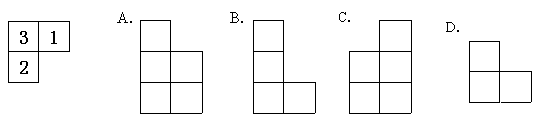
20、由若干个相同的小正方体搭成的几何体的俯视图如图,各小方格内的数字表示
叠在该层位置的小正方体的个数,则这个几何体的左视图是( )
三、解答下列各题:
1、画出下面几何体的三视图.

2、画出底面边长为1cm的正方形,侧棱长为2cm的直四
棱柱的表面展开图,并计算这个直四棱柱的侧面积和体积.
3、截去一个立方体的一个角,得到一个新的几何体,这个新的几何体可能有多少个面?多少个顶点?多少条棱?
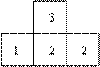 4、由若干个小立方体叠成的几何体的俯视图如图所示,每个方格上的数字表示该位置上叠起的小立方体的个数,请画出几何体的主视图和左视图。
4、由若干个小立方体叠成的几何体的俯视图如图所示,每个方格上的数字表示该位置上叠起的小立方体的个数,请画出几何体的主视图和左视图。
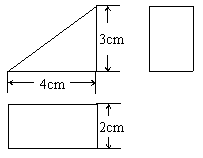 5、已知一个几何体的三视图和有关的尺寸如图所示,求出这
5、已知一个几何体的三视图和有关的尺寸如图所示,求出这
个几何体的表面积.按1:2的比例画出这个几何体的表面展开图.
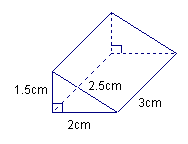 |
6、画出如图所示的底面为直角三角形的直棱柱的表面
展开图,并计算它的侧面积和表面积.
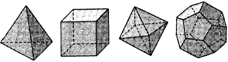
7、新年晚会,是我们最快乐的时候.会场上,悬挂着五彩缤纷的小装饰,其中有种种各样的立体图形.
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) | V+F-E |
| 正四面体 | 4 | 4 | 6 | 2 |
| 正方体 | ||||
| 正八面体 | ||||
| 正十二面体 |
(1)数一下每一个多面体具有的顶点数(V)、棱数(E)和面数(F),并且把结果记入表中.
(2)分析上面的表格,你能发现什么结论?
 8、如图,长方体的长、宽、高分别是8cm,4cm,4cm,一只蚂蚁沿着长方体的表面从点A爬到点B,求蚂蚁爬行的最短路径长.
8、如图,长方体的长、宽、高分别是8cm,4cm,4cm,一只蚂蚁沿着长方体的表面从点A爬到点B,求蚂蚁爬行的最短路径长.
9、用小立方体搭成一个几何体,使它的主视图和俯视图如图所示.搭建这样的几何体,最多要几个小立方体?最少要几个小立方体?